Question

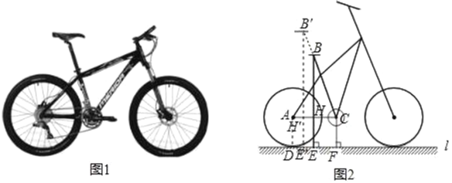
【题目】平面直角坐标系中，C（0，4），A为x轴上一动点，连接AC，将AC绕A点顺时针旋转90°得到AB，当点A在x轴上运动时，OB+BC的最小值为_____．

Answer 1

【答案】

【解析】

过点B作BE⊥x轴，由旋转可知AC=AB，易证△ACO≌△BAE，则AE=OC=4，OA=BE，作点O关于BE的对称点D，则BE垂直平分OD，得到OB=BD，当点C、B、D三点共线时OB+BC=BD+BC=CD，然后设点A坐标为（x，0），则OA=x（），则点E为（x+4，0），则点D为（2x+8，0），得到OD=2x+8，利用勾股定理求出CD，结合二次函数的性质，即可得到CD的最小值，即可解决问题.

解：过点B作BE⊥x轴，

∴∠AEB=∠COA=90°，

∵将AC绕A点顺时针旋转90°得到AB，

∴∠CAB=90°，AC=AB，

∴∠OCA+∠CAO=∠CAO+∠BAE=90°，

∴∠OCA=∠BAE，

∴△ACO≌△BAE，

∴CO=AE=4，OA=BE，

如图，作点O关于BE的对称点D，则BE垂直平分OD，

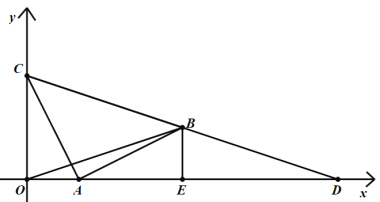
∴OB=DB，

∴当点C、B、D三点共线时OB+BC=BD+BC=CD，OB+BC的最小值为CD；

设点A坐标为（x，0），则OA=x（），

∴点E为（x+4，0），则点D为（2x+8，0），

∴OD=2x+8，

在直角三角形OCD中，由勾股定理，得：，

∴，

∵，

∴当时，CD有最小值，

CD的最小值为：，

∴OB+BC的最小值为：.