题目内容
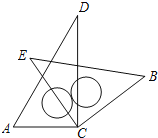
【题目】将一副三角板如图1摆放在直线MN上，在三角板OAB和三角板OCD中，
，
，
．
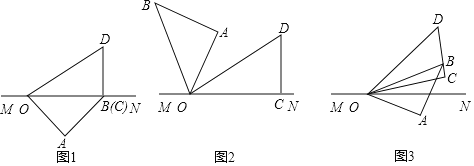
保持三角板OCD不动，将三角板OAB绕点O以每秒
的速度逆时针旋转，旋转时间为t秒．
当
______秒时，OB平分
此时
______
；
当三角板OAB旋转至图2的位置，此时
与
有怎样的数量关系？请说明理由；
如图3，若在三角板OAB开始旋转的同时，另一个三角板OCD也绕点O以每秒
的速度逆时针旋转，当OB旋转至射线OM上时同时停止．
当t为何值时，OB平分
？
直接写出在旋转过程中，与之间的数量关系．
【答案】（1）①
，
②（2）①2②当
时，
，当
时，
，当
时，
【解析】
该小题是简单的旋转问题，结合图1即可求得t的值及
与
的关系
该小题第二问涉及角的旋转问题，利用特殊角解决本题就好做多了
平分
时，根据角平分线的定义即可建立等量关系
，
当
时，即
，
故答案为
，
由题意：
，
，
，
所以t为2时，OB平分
当时，
当时，
当时，
练习册系列答案
新编小学单元自测题系列答案
字词句段篇系列答案
相关题目
