题目内容
【题目】点D,E分别是△ABC的边AB,AC的中点.
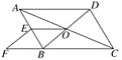
(1)如图1,点O是△ABC内的动点,点O,F分别是OB,OC的中点,求证:DEFG是平行四边形;
(2)如图2,若BE交DC于点O,请问AO的延长线经过BC的中点吗?为什么?

【答案】(1)见解析;(2)见解析.
【解析】
(1)由三角形中位线定理得出DE∥GF,DE=GF,即可得出结论;
(2)由三角形的重心定理即可得出结论.
(1)∵D、E分别是△ABC的边AB、AC的中点,
∴DE是△ABC的中位线,
∴DE∥BC,BC=2DE,
同理:GF∥BC,BC=2GF,
∴DE∥GF,DE=GF,
∴四边形DEFG是平行四边形;
(2) AO的延长线经过BC的中点;理由如下:
∵BE、CD是△ABC的中线,BE交DC于点O,三角形的三条中线相交于一点,
∴AO的延长线经过BC的中点.

练习册系列答案
相关题目
【题目】某商场对某种商品进行销售,第x天的销售单价为m元/件,日销售量为n件,其中m,n分别是x(1≤x≤30,且x为整数)的一次函数,销售情况如表:
销售第x天 | 第1天 | 第2天 | 第3天 | 第4天 | … | 第30天 |
销售单价m(元/件) | 49 | 48 | 47 | 46 | … | 20 |
日销售量n(件) | 45 | 50 | 55 | 60 | … | 190 |
(1)观察表中数据,分别直接写出m与x,n与x的函数关系式: , ;
(2)求商场销售该商品第几天时该商品的日销售额恰好为3600元?
(3)销售商品的第15天为儿童节,请问:在儿童节前(不包括儿童节当天)销售该商品第几天时该商品的日销售额最多?商场决定将这天该商品的日销售额捐献给儿童福利院,试求出商场可捐款多少元?