题目内容
已知关于x的方程
(1)求证:不论k取什么实数值,这个方程总有实数根;(4分)
(2)若等腰三角形ABC的一边长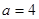 ,另两边的长b,c恰好是这个方程的两根,求△ABC的周长。(8分)
,另两边的长b,c恰好是这个方程的两根,求△ABC的周长。(8分)

(1)求证:不论k取什么实数值,这个方程总有实数根;(4分)
(2)若等腰三角形ABC的一边长
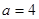 ,另两边的长b,c恰好是这个方程的两根,求△ABC的周长。(8分)
,另两边的长b,c恰好是这个方程的两根,求△ABC的周长。(8分)(1)⊿=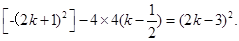 ·····2分
·····2分
∵论k取什么实数值,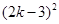 ≥0,·∴原方程总有实数根.
≥0,·∴原方程总有实数根.
(2)∵三角形ABC是等腰三角形ABC,
∴有两条边相等。
若b=c,
∵b、c都是方程的根,
∴⊿=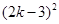 =0,
=0,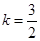 。
。
∴b+c="2k+1=3+1=4."
∵a=4,这时b+c=a,不合题意;
∴不存在这种情况。·若b、c中有一条与a相等,不妨设b=a=4.
∵b是所给的方程的根,
∴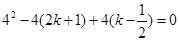 ,∴
,∴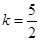 , b+c=2k+1=6,c="2."
, b+c=2k+1=6,c="2."
∵a+b=8>c,
∴三角形ABC的周长为a+b+c=8+2=10.
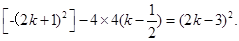 ·····2分
·····2分∵论k取什么实数值,
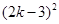 ≥0,·∴原方程总有实数根.
≥0,·∴原方程总有实数根.(2)∵三角形ABC是等腰三角形ABC,
∴有两条边相等。
若b=c,
∵b、c都是方程的根,
∴⊿=
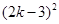 =0,
=0,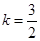 。
。∴b+c="2k+1=3+1=4."
∵a=4,这时b+c=a,不合题意;
∴不存在这种情况。·若b、c中有一条与a相等,不妨设b=a=4.
∵b是所给的方程的根,
∴
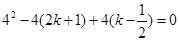 ,∴
,∴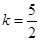 , b+c=2k+1=6,c="2."
, b+c=2k+1=6,c="2." ∵a+b=8>c,
∴三角形ABC的周长为a+b+c=8+2=10.
(1)先把方程化为一般式:x2-(2k+1)x+4k-2=0,要证明无论k取任何实数,方程总有两个实数根,即要证明△≥0;
(2)先利用因式分解法求出两根:x1=2,x2=2k-1.先分类讨论:若a=4为底边;若a=4为腰,分别确定b,c的值,求出三角形的周长.
(2)先利用因式分解法求出两根:x1=2,x2=2k-1.先分类讨论:若a=4为底边;若a=4为腰,分别确定b,c的值,求出三角形的周长.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案 新编小学单元自测题系列答案
新编小学单元自测题系列答案
相关题目
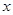 的方程
的方程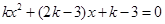 有两个不相等实数根
有两个不相等实数根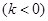 .
.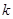 的式子表示方程的两实数根;
的式子表示方程的两实数根;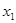 ,
,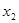 (其中
(其中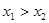 ),且
),且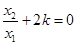 ,求
,求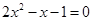 ,变形结果正确的是( ▲ )
,变形结果正确的是( ▲ )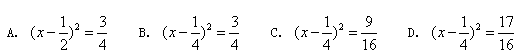
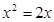 的根是 .
的根是 .
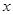 的一元二次方程
的一元二次方程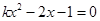 有两个不相等的实数根,则
有两个不相等的实数根,则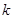 的取值范围是 ( )
的取值范围是 ( )

