题目内容
已知:关于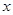 的方程
的方程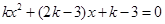 有两个不相等实数根
有两个不相等实数根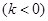 .
.
(1) 用含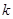 的式子表示方程的两实数根;
的式子表示方程的两实数根;
(2)设方程的两实数根分别是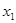 ,
,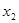 (其中
(其中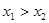 ),且
),且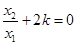 ,求
,求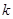 的值.
的值.
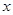 的方程
的方程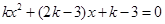 有两个不相等实数根
有两个不相等实数根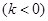 .
.(1) 用含
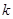 的式子表示方程的两实数根;
的式子表示方程的两实数根;(2)设方程的两实数根分别是
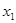 ,
,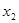 (其中
(其中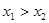 ),且
),且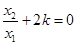 ,求
,求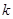 的值.
的值.(I)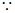 kx2+(2k-3)x+k-3 = 0是关于x的一元二次方程.
kx2+(2k-3)x+k-3 = 0是关于x的一元二次方程.
∴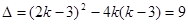
由求根公式,得
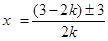 . ∴
. ∴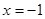 或
或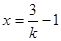
(II)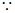
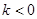 ,∴
,∴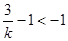 .
.
而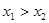 ,∴
,∴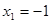 ,
,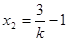 .
.
由题意,有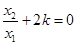
∴ 即
即 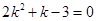 (﹡)
(﹡)
解之,得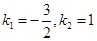
经检验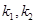 是方程(﹡)的根,但
是方程(﹡)的根,但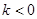 ,∴
,∴
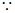 kx2+(2k-3)x+k-3 = 0是关于x的一元二次方程.
kx2+(2k-3)x+k-3 = 0是关于x的一元二次方程.∴
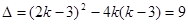
由求根公式,得
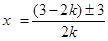 . ∴
. ∴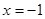 或
或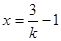
(II)
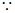
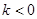 ,∴
,∴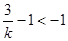 .
. 而
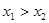 ,∴
,∴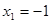 ,
,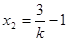 .
. 由题意,有
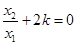
∴
 即
即 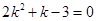 (﹡)
(﹡)解之,得
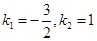
经检验
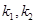 是方程(﹡)的根,但
是方程(﹡)的根,但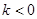 ,∴
,∴
(1)计算△=(2k-3)2-4k(k-3)=9>0,再利用求根公式即可求出方程的两根即可;
(2)有(1)可知方程的两根,再有条件x1>x2,可知道x1和x2的数值,代入计算即可.
(2)有(1)可知方程的两根,再有条件x1>x2,可知道x1和x2的数值,代入计算即可.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目

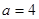 ,另两边的长b,c恰好是这个方程的两根,求△ABC的周长。(8分)
,另两边的长b,c恰好是这个方程的两根,求△ABC的周长。(8分)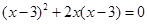 ;
; 
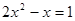
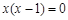 的解是( )
的解是( )


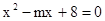 的一个解,则m的值是( )
的一个解,则m的值是( )