题目内容
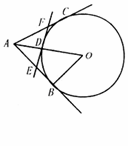
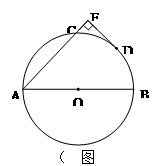
已知:如图,AB为⊙O的直径,AD为弦,∠DBC =∠A.
小题1:求证:BC是⊙O的切线;
小题2:若OC∥AD,OC交BD于E,BD=6,CE=4,求AD的长.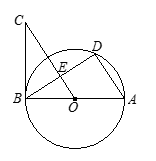
小题1:求证:BC是⊙O的切线;
小题2:若OC∥AD,OC交BD于E,BD=6,CE=4,求AD的长.

小题1:证明:(1)∵AB为⊙O的直径
∴ÐD=90°, ÐA+ÐABD=90°
∵∠DBC =∠A
∴∠DBC+∠ABD=90°
∴BC⊥AB
∴BC是⊙O的切线
小题2:∵OC∥AD,ÐD=90°,BD=6
∴OC⊥BD
∴BE=
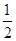 BD="3 "
BD="3 " ∵O是AB的中点
∴AD="2EO " -
∵BC⊥AB ,OC⊥BD
∴△CEB∽△BEO,∴
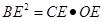
∵CE=4, ∴
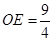
∴AD=
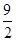
略

练习册系列答案
 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目
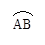
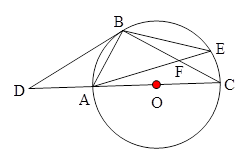
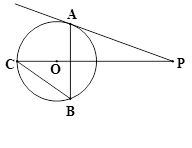
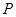 在半径等于3的
在半径等于3的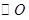 上,则
上,则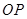 的长( )
的长( )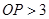
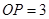
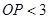
 ?
?