题目内容
【题目】如图在直角坐标系中,四边形ABCO为正方形,A点的坐标为(a,0),D点的坐标为(0,b),且a,b满足(a﹣3)2+|b﹣![]() |=0.
|=0.
(1)求A点和D点的坐标;
(2)若∠DAE=![]() ∠OAB,请猜想DE,OD和EB的数量关系,说明理由.
∠OAB,请猜想DE,OD和EB的数量关系,说明理由.
(3)若∠OAD=30°,以AD为三角形的一边,坐标轴上是否存在点P,使得△PAD为等腰三角形,若存在,直接写出有多少个点P,并写出P点的坐标,选择一种情况证明.

【答案】(1)D(0,![]() ),A(3,0);(2)DE=OD+EB; 理由见解析;(3)点P的坐标为:∴P(﹣3,0)或(0,3
),A(3,0);(2)DE=OD+EB; 理由见解析;(3)点P的坐标为:∴P(﹣3,0)或(0,3![]() )或(0,﹣
)或(0,﹣![]() )或(1,0)或(3+2
)或(1,0)或(3+2![]() ,0)或(3﹣2
,0)或(3﹣2![]() ,0).证明见解析.
,0).证明见解析.
【解析】
(1)根据完全平方式和绝对值的非负性确定a,b的值,从而求点的坐标;
(2)在CO的延长线上找一点F,使OF=BE,连接AF,通过△AOF≌△ABE,得到AF=AE,∠OAF=∠BAE,等量代换得到∠DAF=∠EAD,进而证明△AFD≌△AED,从而求解;
(3)分三种情形讨论求解:AD=DP或AD=AP或PD=AP,分别画图根据AD和OA的长确定点P的坐标.
(1)∵(a﹣3)2+|b﹣![]() |=0,
|=0,
∴a=3,b=![]() ,
,
∴D(0,![]() ),A(3,0);
),A(3,0);
(2)DE=OD+EB; 理由如下:
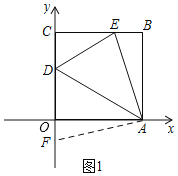
如图1,在CO的延长线上找一点F,使OF=BE,连接AF,
在△AOF和△ABE中,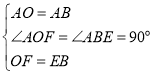 ,
,
∴△AOF≌△ABE(SAS),
∴AF=AE,∠OAF=∠BAE,
又∵∠OAB=90°,∠DAE=![]() ,
,
∴∠BAE+∠DAO=45°,
∴∠DAF=∠OAF+∠DAO=45°,
∴∠DAF=∠EAD,
在△AFD和△AED中,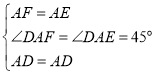 ,
,
∴△AFD≌△AED(SAS),
∴DF=DE=OD+EB;
(3)有3种情况共6个点:
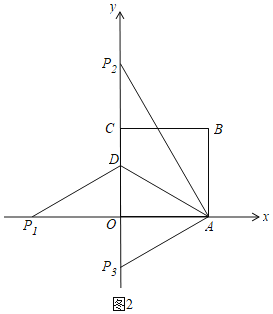
①当DA=DP时,如图2,
Rt△ADO中,OD=![]() ,OA=3,
,OA=3,
∴AD=![]() ,
,
∴P1(﹣3,0),P2(0,3![]() ),P3(0,﹣
),P3(0,﹣![]() );
);
②当AP4=DP4时,如图3,
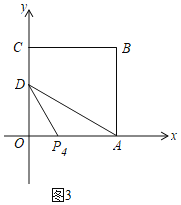
∴∠ADP4=∠DAP4=30°,
∴∠OP4D=60°,
Rt△ODP4中,∠ODP4=30°,OD=![]() ,
,
∴OP4=1,
∴P4(1,0);
③当AD=AP时,如图4,
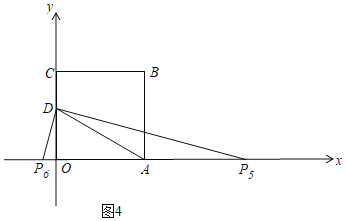
∴AD=AP5=AP6=2![]() ,
,
∴P5(3+2![]() ,0),P6(3﹣2
,0),P6(3﹣2![]() ,0),
,0),
综上,点P的坐标为:∴P(﹣3,0)或(0,3![]() )或(0,﹣
)或(0,﹣![]() )或(1,0)或(3+2
)或(1,0)或(3+2![]() ,0)或(3﹣2
,0)或(3﹣2![]() ,0).
,0).
证明:P5(3+2![]() ,0),
,0),
∵∠OAD=30°且△ADO是直角三角形,
又∵AO=3,DO=![]() ,
,
∴DA=2![]() ,
,
而P5A=|3+2![]() ﹣3|=2
﹣3|=2![]() ,
,
∴P5A=DA,
∴△P5AD是等腰三角形.

【题目】小王某月手机话费中的各项费用统计情况如图表所示,请你根据图表信息完成下列各题
项目 | 月功能费 | 基本话费 | 长途话费 | 短信费 |
金额/元 | 4.8 | 48 |
|
|

(1)请将表格补充完整;
(2)请将条形统计图补充完整;
(3)扇形统计图中,表示短信费的扇形的圆心角是多少度?