题目内容
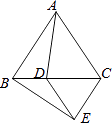
【题目】如图,已知∠1+∠2=180°,∠A=∠C,DA平分∠BDF,试说明BC平分∠DBE.

【答案】证明见解析
【解析】试题分析:由∠2+∠BDC=180°,∠1+∠2=180°可得∠BDC=∠1,所以AE∥FC,所以∠EBC=∠C,又因为∠A=∠C,所以∠EBC=∠A,所以AD∥BC,所以∠ADB=∠CBD,
∠ADF=∠C,所以∠ADF=∠EBC,又因为DA平分∠BDF,所以∠ADB=∠ADF,所以∠CBD=∠EBC,所以BC平分∠DBE.
试题解析:
证明:∵∠2+∠BDC=180°,∠1+∠2=180°,
∴∠BDC=∠1,
∴AE∥FC,
∴∠EBC=∠C,
又∵∠A=∠C,
∴∠EBC=∠A,
∴AD∥BC,
∴∠ADB=∠CBD,∠ADF=∠C,
∴∠ADF=∠EBC,
又∵DA平分∠BDF,
∴∠ADB=∠ADF,
∴∠CBD=∠EBC,
∴BC平分∠DBE.

练习册系列答案
相关题目
【题目】某公司在固定线路上运输,拟用运营指数Q量化考核司机的工作业绩.Q = W + 100,而W的大小与运输次数n及平均速度x(km/h)有关(不考虑其他因素),W由两部分的和组成:一部分与x的平方成正比,另一部分与x的n倍成正比.试行中得到了表中的数据.
次数n | 2 | 1 |
速度x | 40 | 60 |
指数Q | 420 | 100 |
(1)用含x和n的式子表示Q;
(2)当x = 70,Q = 450时,求n的值;
(3)若n = 3,要使Q最大,确定x的值;
(4)设n = 2,x = 40,能否在n增加m%(m>0)同时x减少m%的情况下,而Q的值仍为420,若能,求出m的值;若不能,请说明理由.