题目内容
【题目】立定跳远是小刚同学体育中考的选考项目之一．某次体育课上，体育老师记录了小刚的一组立定跳远训练成绩如下表：
成绩（m） | 2.35 | 2.4 | 2.45 | 2.5 | 2.55 |
次数 | 1 | 1 | 2 | 5 | 1 |
则下列关于这组数据的说法中正确的是（ ）
A.众数是2.45
B.平均数是2.45
C.中位数是2.5
D.方差是0.48
【答案】C
【解析】解：A、如图表所示：众数是2.5，故此选项错误； B、平均数是： 
（2.35+2.4+2.45×2+2.5×5+2.55）=2.47（m），故此选项错误；
C、中位数是： 
=2.5，故此选项正确；
D、方差为： [（2.35﹣2.225）2+（2.4﹣2.225）2+…+（2.55﹣2.225）2]
= （0.015625+0.030625+0.050625+0.378125+0.105625）
=0.0580625，故此选项错误；
故选：C．
利用方差的定义、以及众数和中位数的定义分别计算得出答案．
练习册系列答案
相关题目
【题目】如图，正方形ABCD内部有若干个点，用这些点以及正方形ABCD的顶点A、B、C、D把原正方形分割成一些三角形（互相不重叠）：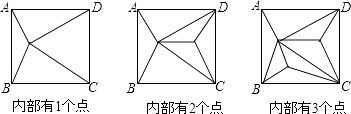
（1）填写如表：
正方形ABCD内点的个数 | 1 | 2 | 3 | 4 | … | n |
分割成的三角形的个数 | 4 | 6 | … |
（2）如果原正方形被分割成2016个三角形，此时正方形ABCD内部有多少个点？
（3）上述条件下，正方形又能否被分割成2017个三角形？若能，此时正方形ABCD内部有多少个点？若不能，请说明理由．
（4）综上结论，你有什么发现？（写出一条即可）
