Question

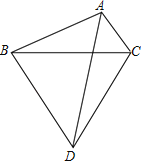
【题目】如图，在△ABC中，∠BAC＝120°，以BC为边向外作等边△BCD.

(Ⅰ)∠ABD+∠ACD＝_____.

(Ⅱ)∠BAD＝_____.

(Ⅲ)若AB＝3，AC＝2，求AD的长.

Answer 1

【答案】(Ⅰ)180°；(Ⅱ)60°；(Ⅲ)AD＝5.

【解析】

(Ⅰ)根据四边形内角和360°可求；

(Ⅱ)将△ACD绕点D逆时针旋转60°，得到△BED，证明A、B、E三点共线，所以△ADE是等边三角形，则∠BAD＝60°；

(Ⅲ)根据BE＝AC＝2，则AE＝AB+BE＝3+2＝5，则等边△ADE的边AD＝5.

(Ⅰ)因为四边形内角和360°，

所以∠BAD+∠BDC+∠ABD+∠ACD＝360°，

∴∠ABD+∠ACD＝360°﹣120°﹣60°＝180°.

故答案为180°；

(Ⅱ)将△ACD绕点D逆时针旋转60°，得到△BED(如图所示)，

∵DC＝BD，∠BDC＝60°，

∴旋转后的三角形DC与BD重合.

又∠ABD+∠ACD＝180°，

所以∠ABD+∠EBD＝180°，

∴A、B、E三点共线.

所以△ADE是等边三角形，

∴∠BAD＝60°.

故答案为60°；

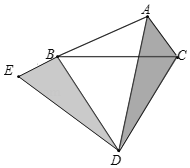
(Ⅲ)根据(Ⅱ)可知BE＝AC＝2，则AE＝AB+BE＝3+2＝5.

所以AD＝5.

故答案为180°，60°.