题目内容
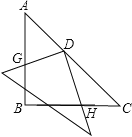
【题目】如图所示：一副三角板如图放置，等腰直角三角板ABC固定不动，另一块三角板的直角顶点放在等腰直角三角形的斜边中点D处，且可以绕点D旋转，在旋转过程中，两直角边的交点G、H始终在边AB、BC上．
在旋转过程中线段BG和CH大小有何关系？证明你的结论．
若
，在旋转过程中四边形GBHD的面积是否改变？若不变，求出它的值；若改变，求出它的取值范围．
若交点G、H分别在边AB、BC的延长线上，则中的结论仍然成立吗？请画出相应的图形，直接写出结论．
【答案】
BG=CH，证明见解析；
在旋转过程中四边形GBHD的面积不变，
；
见解析.
【解析】
连接BD，根据等腰直角三角形的性质，得，
，
，
，由
，
，推出
后，结合
，即可推出
≌
，根据全等三角形的性质可得
；
首先根据题意求出
，然后通过求证
≌
，由的结论，即可推出
，再根据
，，推出
，即得，
，便可确定在旋转过程中四边形GBHD的面积不变；
连接BD后，首先通过余角的性质推出
，再根据
，推出
，即可推出
和
，便可得．
和CH为相等关系，
如图1，连接BD，
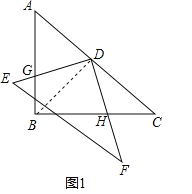
等腰直角三角形ABC，D为AC的中点，
，
，，
，
，
，
，
在和中，
，
≌
，
，
，
，
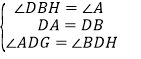等腰直角三角形ABC，D为AC的中点，
，，，
，
，
，
，
在和中，
，
≌
，
，
，，
，
，
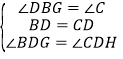在旋转过程中四边形GBHD的面积不变，
当三角板DEF旋转至图2所示时，的结论仍然成立，
如图2，连接BD，
，
，
，
，
，
，
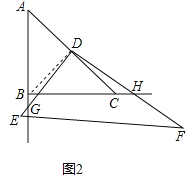
等腰直角三角形ABC，
，
，
在和中，
，
≌
，
．
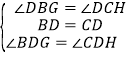练习册系列答案
相关题目
