题目内容
【题目】如图，△A1B1C1中，A1B1＝4，A1C1＝5，B1C1＝7.点A2，B2，C2分别是边B1C1，A1C1，A1B1的中点；点A3，B3，C3分别是边B2C2，A2C2，A2B2的中点；…；以此类推，则△A4B4C4的周长是________，△AnBnCn的周长是________．
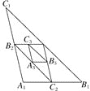
【答案】2 25-n.
【解析】
根据三角形的中位线平行于第三边并且等于第三边的一半可得中点三角形的周长等于原三角形的周长的一半，然后写出前四个三角形的周长，再根据指数的变化规律写出△AnBnCn的周长即可．
解：∵A1B1=4，A1C1=5，B1C1=7，
∴△A1B1C1的周长=4+5+7=16，
∵依次连接△A1B1C1三边中点，得△A2B2C2，
∴△A2B2C2的周长=
×16=
=8，
∵再依次连接△A2B2C2的三边中点，得△A3B3C3，
∴△A3B3C3的周长=×(×16)=
=4，
∵再依次连接△A3B3C3的三边中点，得△A4B4C4，
∴△A4B4C4的周长=××(×16)=
=2，
…，
△AnBnCn的周长=
×16=
=25-n.
故答案为：2；25-n.
练习册系列答案
相关题目
