Question

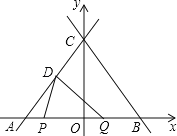
【题目】已知：如图，在Rt△ABC中，∠C＝90°，沿过B点的一条直线BE折叠这个三角形， 使C点与AB边上的一点D重合．

(1)当∠A满足什么条件时，点D恰为AB的中点?写出一个你认为适当的条件，并利用此条件证明D为AB的中点；

(2)在(1)的条件下，若DE＝1，求△ABC的面积．

Answer 1

【答案】（1）∠A=30°；（2）．

【解析】试题分析：（1）根据折叠的性质：△BCE≌△BDE，BC=BD，当点D恰为AB的中点时，AB=2BD=2BC，又∠C=90°，故∠A=30°；当添加条件∠A=30°时，由折叠性质知：∠EBD=∠EBC=30°，又∠A=30°且ED⊥AB，可证：D为AB的中点；

（2）在Rt△ADE中，根据∠A，ED的值，可将AE、AD的值求出，又D为AB的中点，可得AB的长度，在Rt△ABC中，根据AB、∠A的值，可将AC和BC的值求出，代入S△ABC=AC×BC进行求解即可．

解：（1）添加条件是∠A=30°．

证明：∵∠A=30°，∠C=90°，所以∠CBA=60°，

∵C点折叠后与AB边上的一点D重合，

∴BE平分∠CBD，∠BDE=90°，

∴∠EBD=30°，

∴∠EBD=∠EAB，所以EB=EA；

∵ED为△EAB的高线，所以ED也是等腰△EBA的中线，

∴D为AB中点．

（2）∵DE=1，ED⊥AB，∠A=30°，∴AE=2．

在Rt△ADE中，根据勾股定理，得AD==，

∴AB=2，∵∠A=30°，∠C=90°，

∴BC=AB=．

在Rt△ABC中，AC==3，

∴S△ABC=×AC×BC=．