��Ŀ����
����Ŀ����������С��ͬ�ĺ�30���ǵ����ǰ��ֱ�Ƕ���O�غ���һ�𣬱�����COD����������AOB�Ƶ�O��ת��������AB������DC���ڵ�F��
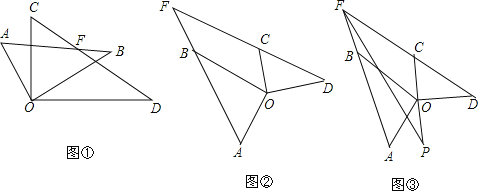
��1����ͼ�٣�����AOD=120�㣬
��AB��OD��λ�ù�ϵ ��
�ڡ�AFC�Ķ���= ��
��2����ͼ�ڵ���AOD=130�������AFC�Ķ�����
��3�������������д����AOD�͡�AFC�Ĺ�ϵ ��
��4����ͼ�ۣ�����AFC����AOD�Ľ�ƽ���߽��ڵ�P�����P�Ķ�����
���𰸡�(1)��AB��OD����30�㣻��2��40�㣻��3����AOD=��AFC+90������4��15��.
��������
��1�����������BOD=30�����Ӷ��õ���B=��BOD���ٸ����ڴ�����ȣ���ֱ��ƽ�н��
�ڸ�����ֱ��ƽ�У�ͬλ����Ƚ�ɣ�
��2�������ܽ������BOC�������ڲ��������OBF�͡�OCF��Ȼ������ı��ε��ڽǺͶ�����ʽ���㼴�ɵý⣻
��3�����ݼ���Ķ���д����ϵʽ���ɣ�
��4����OB��PF�ཻ��G��Ȼ����������ε��ڽǺͶ�����ʽ�������ɵý⣮
��1���١ߡ�AOD=120�㣬
���BOD=��AOD-��AOB=120��-90��=30�㣻
���B=��BOD��
��AB��OD��
�ڡ�AB��OD��
���AFC=��D=30�㣻
��2���ߡ�AOD=130�㣬
���BOC=360��-130��-90���2=50�㣬
�֡ߡ�OBF=180��-30��=150�㣬��OCF=180��-60��=120�㣬
���AFC=360��-150��-120��-50��=40�㣻
��3����AOD=��AFC+90�㣻
��4����OB��PF�ཻ��G��
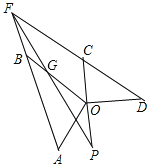
�ߡ�AFC����AOD�Ľ�ƽ���߽��ڵ�P��
���BFG=![]() ��AFC����AOP=
��AFC����AOP=![]() ��AOD��
��AOD��
����BFG����OGP����BFG+��OBF=��POG+��P��
��![]() ��AFC+150��=
��AFC+150��=![]() ��AOD+90��+��P��
��AOD+90��+��P��
��![]() ��AFC+150��=
��AFC+150��=![]() ����AFC+90�㣩+90��+��P��
����AFC+90�㣩+90��+��P��
�����ã���P=15�㣮