��Ŀ����
����Ŀ����ͼ�٣�BD�Ǿ���ABCD�ĶԽ��ߣ���ABD=30�㣬AD=1������BCD������BD����ƽ�Ƶ���B'C'D'��λ�ã�ʹB'ΪBD�е㣬����AB'��C'D��AD'��BC'����ͼ�ڣ�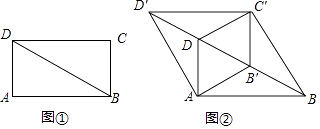
��1����֤���ı���AB'C'D�����Σ�
��2���ı���ABC'D����ܳ�Ϊ��
��3�����ı���ABC'D'�����������Խ��������õõ����ĸ�������ƴ�����������ȵľ��Σ�ֱ��д�����п���ƴ�ɵľ����ܳ���
���𰸡�
��1���⣺��BD�Ǿ���ABCD�ĶԽ��ߣ���ABD=30�㣬
���ADB=60�㣬
��ƽ�ƿɵã�B'C'=BC=AD����D'B'C'=��DBC=��ADB=60�㣬
��AD��B'C'
���ı���AB'C'D��ƽ���ı��Σ�
��B'ΪBD�е㣬
��Rt��ABD��AB'= ![]() BD=DB'��
BD=DB'��
�֡ߡ�ADB=60�㣬
���ADB'�ǵȱ������Σ�
��AD=AB'��
���ı���AB'C'D�����Σ�
��2��4 ![]()
��3���⣺���ı���ABC'D'�����������Խ��������õõ����ĸ�������ƴ�����������ȵľ������£�
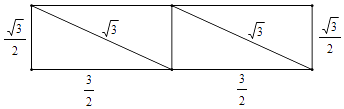

������ܳ�Ϊ6+ ![]() ��2
��2 ![]() +3��
+3��
����������2����ƽ�ƿɵã�AB=C'D'����ABD'=��C'D'B=30�㣬
��AB��C'D'��
���ı���ABC'D'��ƽ���ı��Σ�
�ɣ�1���ɵã�AC'��B'D��
���ı���ABC'D'�����Σ�
��AB= ![]() AD=
AD= ![]() ��
��
���ı���ABC'D����ܳ�Ϊ4 ![]() ��
��
���Դ��ǣ�4 ![]() ��
��
�����㾫����������Ĺؼ�����������ε����ʵ����֪ʶ�����վ��ε��ĸ��Ƕ���ֱ�ǣ����εĶԽ�����ȣ��Լ���ƽ�Ƶ����ʵ����⣬�˽�پ���ƽ��֮���ͼ����ԭ����ͼ�εĶ�Ӧ�߶�ƽ�У�����ͬһֱ���ϣ�����ȣ���Ӧ����ȣ�ͼ�ε���״���С��û�з����仯���ھ���ƽ�ƺ�Ӧ���������߶�ƽ�У�����ͬһֱ���ϣ�����ȣ�