题目内容
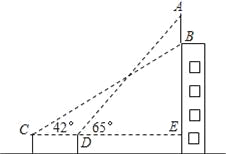
【题目】如图,某大楼顶部有一旗杆AB,甲乙两人分别在相距6米的C、D两处测得B点和A点的仰角分别是42°和65°,且C、D、E在一条直线上.如果DE=15米,求旗杆AB的长大约是多少米?(结果保留整数)
(参考数据:sin42°≈0.67,tan42°≈0.9,sin65°≈0.91,tan65°≈2.1)
【答案】旗杆AB的长大约是13米
【解析】试题分析:根据题意构造直角三角形,在两个直角三角形△ADE、△CBE求得AE、BE的长,再利用AB=AE-BE可求出答案.
试题解析:
在直角△ADE中,∠ADE=65°,DE=15米,则tan∠ADE=![]() ,sin∠ADE=
,sin∠ADE=![]() ,
,
即tan65°=![]() ≈2.1,解得 AE≈31.5(米),
≈2.1,解得 AE≈31.5(米),
在直角△BCE中,∠BCE=42°,CE=CD+DE=21米,则tan∠BCE=![]() ,即tan42°=
,即tan42°=![]() ≈0.9,
≈0.9,
解得 BE≈18.9(米),则AB=AE﹣BE=31.5﹣18.9≈13(米).
答:旗杆AB的长大约是13米.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
【题目】商场某柜台销售每台进价分别为160元、120元的A、B两种型号的电风扇,下表是近两周的销售情况:
销售时段 | 销售数量 | 销售收入 | |
A种型号 | B种型号 | ||
第一周 | 3台 | 4台 | 1200元 |
第二周 | 5台 | 6台 | 1900元 |
(进价、售价均保持不变,利润=销售收入﹣进货成本)
(1)求A、B两种型号的电风扇的销售单价;
(2)若商场准备用不多于7500元的金额再采购这两种型号的电风扇共50台,求A种型号的电风扇最多能采购多少台?
(3)在(2)的条件下,商场销售完这50台电风扇能否实现利润超过1850元的目标?若能,请给出相应的采购方案;若不能,请说明理由.