题目内容
【题目】如图,正△ABC的边长为2,以BC边上的高AB1为边作正△AB1C1 , △ABC与△AB1C1公共部分的面积记为S1;再以正△AB1C1边B1C1上的高AB2为边作正△AB2C2 , △AB1C1与△AB2C2公共部分的面积记为S2;…,以此类推,则Sn= . (用含n的式子表示) 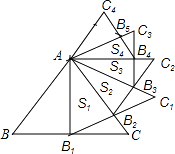
【答案】![]() (
( ![]() )n
)n
【解析】解:∵等边三角形ABC的边长为2,AB1⊥BC,
∴BB1=1,AB=2,
根据勾股定理得:AB1= ![]() ,
,
∴S1= ![]() ×
× ![]() ×(
×( ![]() )2=
)2= ![]() (
( ![]() )1;
)1;
∵等边三角形AB1C1的边长为 ![]() ,AB2⊥B1C1,
,AB2⊥B1C1,
∴B1B2= ![]() ,AB1=
,AB1= ![]() ,
,
根据勾股定理得:AB2= ![]() ,
,
∴S2= ![]() ×
× ![]() ×(
×( ![]() )2=
)2= ![]() (
( ![]() )2;
)2;
依此类推,Sn= ![]() (
( ![]() )n.
)n.
故答案为: ![]() (
( ![]() )n.
)n.
由AB1为边长为2的等边三角形ABC的高,利用三线合一得到B1为BC的中点,求出BB1的长,利用勾股定理求出AB1的长,进而求出S1,同理求出S2,依此类推,得到Sn.

练习册系列答案
相关题目
【题目】某课外小组的同学们在社会实践活动中调查了20户家庭某月的用电量,如下表所示:则这20户家庭该月用电量的众数和中位数分别是( )
用电量(度) | 120 | 140 | 160 | 180 | 200 |
户数 | 2 | 3 | 6 | 7 | 2 |
A.7,6B.7,3C.180,160D.180,170




