Question

【题目】如图1，在中，，，，点D，E分别在边BC，AC上．

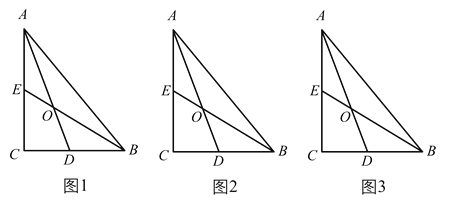
当时，直接写出______，______；

如图2，若O为AD的中点，求证：；

如图3，当，时，求AE的值．

Answer 1

【答案】（1） ；（2）见解析；（3） ．

【解析】

（1）如图1中，作AF∥BC交BE的延长线于F．利用平行线分线段成比例定理，一一求解即可．
（2）如图2中，作DF∥AC交BF于F．利用平行线分线段成比例定理即可解决问题．
（3）如图3中，作EF⊥AB于F．设AE=5k，BD=3k．只要证明△ACD∽△BFE，可得 ，可得 ，解方程即可解决问题．

（1）解：如图1中，作AF∥BC交BE的延长线于F．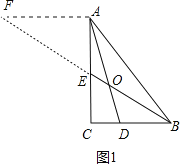

∵AF∥BC，
∴ ，
∵AE=2，AC=4，
∴AE=EC，AF=BC=3，EF=BE，设EF=EB=b，
∵AF∥DB，
∴ ，
∴OF= b，OB= b，
∴OE=OF-EF=b，
∴ ，
故答案为 ．
（2）证明：如图2中，作DF∥AC交BF于F．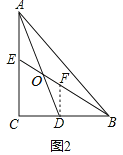

∵DF∥AE，OA=OD，
∴=1
∴AE=DF，
∵DF∥EC，
∴，
∴．
（3）解：如图3中，作EF⊥AB于F．设AE=5k，BD=3k．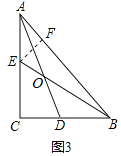

∵∠ACB=90°，AC=4，BC=3，
∴AB= =5，
∵∠EAF=∠CAB，∠AFE=∠C=90°，
∴△AEF∽△ABC，
∴ ，
∴AF=4k，EF=3k，
∵∠AOE=∠BAC，
∴∠OAB+∠OBA=∠CAD+∠OAB，
∴∠CAD=∠ABO，∵∠C=∠EFB=90°，
∴△ACD∽△BFE，
∴ ，
∴ ，
整理得4k2-13k+5=0，
解得k= 或（舍弃），
∴AE=5k= ．