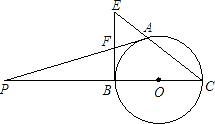题目内容
【题目】如图,在⊙O中,AB是⊙O的直径,AC是⊙O的弦,过点C作⊙O的切线交BA的延长线于点P,连接BC. 
(1)求证:∠PCA=∠B;
(2)填空:已知∠P=40°,AB=12cm,点Q在 ![]() 上,从点A开始以πcm/s的速度逆时针运动到点C停止,设运动时间为ts. ①当t=时,以点A、Q、B、C为顶点的四边形面积最大;
上,从点A开始以πcm/s的速度逆时针运动到点C停止,设运动时间为ts. ①当t=时,以点A、Q、B、C为顶点的四边形面积最大;
②当t=时,四边形AQBC是矩形.
【答案】
(1)证明:如图1中,连接OC.

∵PC是切线,OC是半径,
∴OC⊥PC,
∴∠PCO=90°
∴∠PCA+∠ACO=90°,
∵AB是直径,
∴∠ACB=90°,
∴∠B+∠CAB=90°,
∵OC=OA,
∴∠OAC=∠OCA,
∴∠B+∠OCA=90°,
∴∠PCA=∠B.
(2)3s;![]()
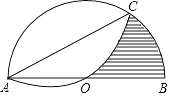
【解析】解:(2)①如图2中,当点Q在AB下方, ![]() =
= ![]() 时,四边形AQBC的面积最大,此时t=
时,四边形AQBC的面积最大,此时t= ![]() =3s.
=3s. 
所以答案是3s.
②如图3中,当 ![]() =
= ![]() 时,四边形AQBC是矩形,连接CQ与AB交于点O.
时,四边形AQBC是矩形,连接CQ与AB交于点O.
∵∠P=40°,∠PCO=90°,
∴∠POC=50°,
∴∠AOQ=130°,
∴弧AQ的长= ![]() =
= ![]() ,
,
∴t= ![]() =
= ![]() s.
s.
所以答案是 ![]() s.
s.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
【题目】九(1)班数学兴趣小组经过市场调查,整理出某种商品在第x(1≤x≤90)天的售价与销量的相关信息如下表:
时间x(天) | 1≤x<50 | 50≤x≤90 |
售价(元/件) | x+40 | 90 |
每天销量(件) | 200﹣2x | |
已知该商品的进价为每件30元,设销售该商品的每天利润为y元.
(1)求出y与x的函数关系式;
(2)问销售该商品第几天时,当天销售利润最大,最大利润是多少?
(3)该商品在销售过程中,共有多少天每天销售利润不低于4800元?请直接写出结果.