题目内容
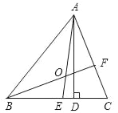
【题目】如图所示，在△ABC中，AD是高，AE、BF是角平分线，它们相交于点O，∠BAC＝60°，∠C＝70°，求∠DAE、∠BOA的度数．
【答案】∠DAE，∠BOA的度数分别是10°，125°
【解析】
根据角平分线的定义可得∠BAE=∠CAE=
∠BAC=30°，在Rt△ADC中可求得∠CAD的度数，再根据∠DAE=∠CAE﹣∠CAD即可得解，根据三角形的内角和可得∠ABC的度数，即可得∠ABO的度数，再在△AOB中利用三角形的内角和为180°即可求得∠BOA的度数.
解∵AD⊥BC，
∴∠ADC＝90°，
∵∠C＝70°，
∴∠CAD＝180°﹣90°﹣70°＝20°，
∵∠BAC＝60°，AE是∠BAC的角平分线，
∴∠EAC＝∠BAE＝30°，
∴∠EAD＝∠EAC﹣∠CAD＝30°﹣20°＝10°，
∠ABC＝180°﹣∠BAC﹣∠C＝50°，
∵BF是∠ABC的角平分线，
∴∠ABO＝25°，
∴∠BOA＝180°﹣∠BAO﹣∠ABO＝180°﹣30°﹣25°＝125°．
故∠DAE，∠BOA的度数分别是10°，125°
练习册系列答案
相关题目
【题目】六盘水市梅花山国际滑雪自建成以来，吸引大批滑雪爱好者，一滑雪者从山坡滑下，测得滑行距离y（单位：cm）与滑行时间x（单位：s）之间的关系可以近似的用二次函数来表示．
滑行时间x/s | 0 | 1 | 2 | 3 | … |
滑行距离y/cm | 0 | 4 | 12 | 24 | … |
（1）根据表中数据求出二次函数的表达式．现测量出滑雪者的出发点与终点的距离大约800m，他需要多少时间才能到达终点？
（2）将得到的二次函数图象补充完整后，向左平移2个单位，再向上平移5个单位，求平移后的函数表达式．
