题目内容
【题目】在Rt△ABC中,∠ACB=90°,CD⊥AB于D,∠BAC的平分线AF交CD于点E,交BC于F,CM⊥AF于M,CM的延长线交AB于点N.
(1)求证:EM=FM;
(2)求证:AC=AN.
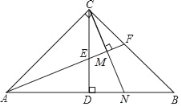
【答案】(1)详见解析;(2)详见解析.
【解析】
(1)根据题意可得∠AED+∠DAE=90°,∠CFE+∠CAE=90°,因为∠BAC的平分线AF交CD于E,所以∠DAE=∠CAE,即∠AED=∠CFE,然后根据等腰三角形判定与性质即可得证;
(2)通过“角边角”证明△AMN≌△AMC,即可得AC=AN.
(1)证明:∵∠ACB=90°,CD⊥AB,
∴∠ADC=90°,
∴∠AED+∠DAE=90°,∠CFE+∠CAE=90°,
又∵∠BAC的平分线AF交CD于E,
∴∠DAE=∠CAE,
∴∠AED=∠CFE,
又∵∠AED=∠CEF,
∴∠CEF=∠CFE,
又∵CM⊥AF,
∴EM=FM.
(2)证明:∵CN⊥AF,
∴∠AMC=∠AMN=90°,
在△AMN和△AMC中,
 ,
,
∴△AMN≌△AMC(SAS),
∴AC=AN.

练习册系列答案
 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案
相关题目