题目内容
【题目】如图，平行四边形ABCD中，A（-1，0）、B（0，-2），顶点C、D在双曲线
（x＞0）上，边AD交y轴于点E，若点E恰好是AD的中点，则k=_____．
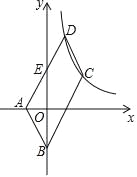
【答案】4
【解析】
根据题意可设点D的坐标为（m，n），则点C的坐标为（m+1，n-2），再根据E为AD中点可得m=1，然后将C，D坐标代入双曲线解析式中，得到关于n的方程，然后解方程即可.
解：根据题意可知：平行四边形ABCD中，A（-1，0）、B（0，-2），
可设点D的坐标为（m，n），则点C的坐标为（m+1，n-2），
∵边AD交y轴于点E，点E恰好是AD的中点，
∴m=1，
∵k=mn=（m+1）（n-2），即k=n=2（n-2），
解得：n=k=4．
故答案为：4．
练习册系列答案
激活思维智能训练课时导学练系列答案
相关题目
