题目内容
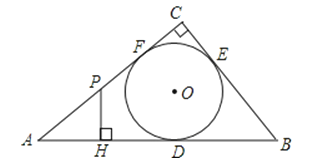
【题目】如图,⊙O是△ABC的内切圆,点D、E分别为边AC、BC上的点,且DE为⊙O的切线,若△ABC的周长为25,BC的长是9,则△ADE的周长是( )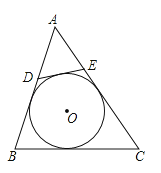
A.7
B.8
C.9
D.16
【答案】A
【解析】解:∵AB、AC、BC、DE都和⊙O相切,
∴BI=BG,CI=CH,DG=DF,EF=EH.
∴BG+CH=BI+CI=BC=9,
∴C△ADE=AD+AE+DE=AD+AE+DF+EF=AD+DG+EH+AE=AG+AH=C△ABC﹣(BG+EH+BC)=25﹣2×9=7.
故选A.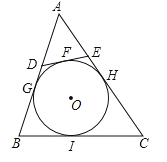
根据切线长定理,可得BI=BG,CI=CH,DG=DF,EF=EH,则C△ADE=AD+AE+DE=AD+AE+DF+EF=AD+DG+EH+AE=AG+AH=C△ABC﹣(BG+EH+BC),据此即可求解.

练习册系列答案
相关题目