题目内容
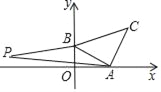
【题目】如图,直线y=﹣![]() x+1与x轴、y轴分别交于点A、B,以线段AB为直角边在第﹣象限内作等腰直角△ABC,∠BAC=90°,
x+1与x轴、y轴分别交于点A、B,以线段AB为直角边在第﹣象限内作等腰直角△ABC,∠BAC=90°,
(1)求点A、B、C的坐标;
(2)如果在第二象限内有﹣点P(a,![]() ),且△ABP的面积与△ABC的面积相等,求a的值;
),且△ABP的面积与△ABC的面积相等,求a的值;
(3)请直接写出点Q的坐标,使得以Q、A、C为顶点的三角形和△ABC全等.
【答案】(1)A(![]() ,0),B(0,1),C(
,0),B(0,1),C(![]() +1,
+1,![]() );(2)a=
);(2)a=![]() ;(3)点Q的坐标为:(1,
;(3)点Q的坐标为:(1,![]() +1 );( 2
+1 );( 2![]() ,﹣1 );( 2
,﹣1 );( 2![]() +1,
+1,![]() ﹣1).
﹣1).
【解析】
(1)由直线解析式可求得A、B的坐标,过C作CD⊥x轴于点D,则可证得△AOB≌△CDA,则可求得CD和AD的长,可求得C点坐标;
(2)过作 PE⊥x 轴于点 E,依据△ABP的面积与△ABC的面积相等,即可得到S△AOB+S梯形BOEP﹣S△AEP=2,得到关于a的方程,从而求得a的值;
(3)依据以Q、A、C为顶点的三角形和△ABC全等,A(![]() ,0),B(0,1),C(
,0),B(0,1),C(![]() +1,
+1,![]() ),即可得到点Q的坐标.
),即可得到点Q的坐标.
(1)根据题意,直线y=﹣![]() x+1与x轴、y轴分别交于A、B,
x+1与x轴、y轴分别交于A、B,
令x=0,则y=1;令y=0,则x=![]() ,
,
即A(![]() ,0),B(0,1),
,0),B(0,1),
即OA=![]() ,OB=1,则AB=2;
,OB=1,则AB=2;
如图,过C作CD⊥AO于D,则∠ADC=∠BOA=90°,
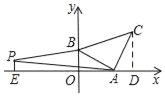
∵△ABC是等腰直角三角形,
∴AB=AC=2,∠BAC=90°,
∴∠BAO=∠ACD,
∴△ABO≌△CAD,
∴AD=BO=1,CD=AO=![]() ,
,
∴C(![]() +1,
+1,![]() );
);
(2)由题可得,S△ABC=![]() ×2×2=2,
×2×2=2,
如图,作 PE⊥x 轴于点 E,则EO=﹣a,PE=![]() ,AE=
,AE=![]() ﹣a,
﹣a,
∵S△ABC=S△ABP=2,
∴S△AOB+S梯形BOEP﹣S△AEP=2,
即![]() ×
×![]() ×1+
×1+![]() ×(
×(![]() +1)×(﹣a)﹣
+1)×(﹣a)﹣![]() ×(
×(![]() ﹣a)×
﹣a)×![]() =2,
=2,
解得a=![]() -4;
-4;
(3)以Q、A、C为顶点的三角形和△ABC全等,A(![]() ,0),B(0,1),C(
,0),B(0,1),C(![]() +1,
+1,![]() ),
),
分三种情况:如图,当点Q在AC左上方时,过Q1作Q1F⊥y轴于F,连接BQ1,
依据△ABO与△BFQ1全等,可得Q1F=BO=1,BF=AO=![]() ,
,
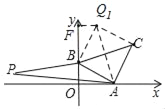
∴Q1(1,![]() +1 );
+1 );
如图,当点Q在AC的右下方时,过Q2作Q2G⊥x轴于G,
依据△AOB与△AGQ2全等,可得Q2G=BO=1,AG=AO=![]() ,
,
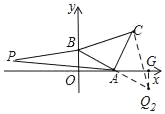
∴Q2( 2![]() ,﹣1 );
,﹣1 );
如图,当点Q在AC的右上方时,过C作CH∥y轴,过Q3作Q3H∥x轴,
依据△AOB与△CHQ3全等,可得Q3H=AO=![]() ,CH=BO=1,而C(
,CH=BO=1,而C(![]() +1,
+1,![]() ),
),
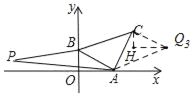
∴Q3( 2![]() +1,
+1,![]() ﹣1).
﹣1).
综上所述,点Q的坐标为:(1,![]() +1 );( 2
+1 );( 2![]() ,﹣1 );( 2
,﹣1 );( 2![]() +1,
+1,![]() ﹣1).
﹣1).

 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案