题目内容
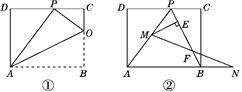
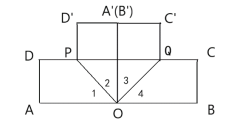
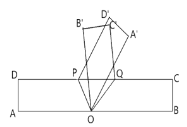
【题目】如图，有一个长方形纸条ABCD，点P，Q是线段CD上的两个动点，且点P始终在点Q左侧，在AB上有一点O，连结PO、QO，以PO，QO为折痕翻折纸条，使点A、点B、点C、点D分别落在点A’、点B’、点C’、点D’上.
（1）当
时，
=_______
（2）当A’O与B’O重合时，
=_________.
（3）当
时，求的度数.
【答案】（1）
；（2）
；（3）
或
.
【解析】
（1）根据折叠性质即可求出答案；
（2）根据折叠性质及平角定义即可求出答案；
（3）分情况讨论：①如图，当A'在B'的左侧时，②如图，当B' 在A'的左侧时，根据角之间的和、差关系，即可求解.
（1）∵∠POA=
,
由折叠性质得：∠A’OP=∠POA=
∴
；
（2）由折叠性质得：∠1=∠2，∠3=∠4，
∴
；
（3） ∵以PO、QO为折痕翻折纸条,
∴设
，
，
∵∠B'OA'=30°，
①如图，当A'在B'的左侧时，
，
即
，
解得
，
∴
；
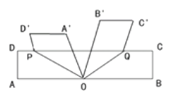
②如图，当B' 在A'的左侧时，
，
即
，
解得：
，
,
综上所述：
为或.
练习册系列答案
相关题目
【题目】如果一个多边形的各边都相等，且各内角也都相等，那么这个多边形就叫做正多边形．如图，就是一组正多边形，观察每个正多边形中∠α的变化情况，解答下列问题：
（1）将下面的表格补充完整：
正多边形边数 | 3 | 4 | 5 | 6 | … | n |
∠α的度数 | 60° | 45° |
|
| … |
|
（2）根据规律，是否存在一个正多边形，其中的∠α＝21°？若存在，请求出n的值，若不存在，请说明理由．
