题目内容
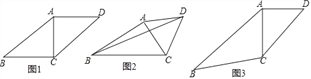
【题目】如果一个多边形的各边都相等，且各内角也都相等，那么这个多边形就叫做正多边形．如图，就是一组正多边形，观察每个正多边形中∠α的变化情况，解答下列问题：
（1）将下面的表格补充完整：
正多边形边数 | 3 | 4 | 5 | 6 | … | n |
∠α的度数 | 60° | 45° |
|
| … |
|
（2）根据规律，是否存在一个正多边形，其中的∠α＝21°？若存在，请求出n的值，若不存在，请说明理由．
【答案】（1）36°，30°，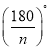
；（2）不存在，理由见解析.
【解析】
（1）根据多边形内角和公式求出多边形每个内角的度数，再根据三角形内角和定理求出即可；
（2）根据（1）中得出的规律，列方程求解即可；
解：（1）当正多边形有5条边时，每个内角度数=(5-2) ×180°÷5=108°，则∠α=(180°-108°) ÷2=36°=180°÷5；
当正多边形有6条边时，每个内角度数=(6-2) ×180°÷6=120°，则∠α=(180°-120°) ÷2=30°=180°÷6；
由以上两个式子可知，当正多边形有n条边时，每个内角度数；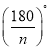
填写下表：
正多边形边数 | 3 | 4 | 5 | 6 | … | n |
∠α的度数 | 60° | 45° | 36° | 30° | … | （ |
（2）不存在，理由如下：
设存在正n边形使得∠α＝21°，
得∠α＝21°＝（
）°．
解得：n＝8
，n是正整数，n＝8（不符合题意要舍去），
不存在正n边形使得∠α＝21°．
【题目】公园的门票价格规定如下表：
购票张数 | 1 到 50 张 | 51 到 100 张 | 101 到 150张 | 150 张以上 |
每张票的价格 | 12 元 | 10 元 | 8 元 | 超过 150 张的部分 7 元 |
某校七年级（1）（2）两个班共 104 人，其中（1）班 40 多人，不足 50 人，经估算，如果两个班都以班为单位购票，则一共应付 1136 元，问：
(1)若两班联合起来作为一个团体购票，可省多少钱？
(2)两班学生各有多少人？
(3)若七年级（3）班有 n 人（46<n<55）与（1）,（2）班一起去游园，某商家赞助，支付三个班的所有门票费，则该商家最少花费 元（用含 n 的式子表示）
