��Ŀ����
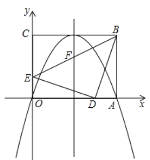
����Ŀ��ƽ��ֱ������ϵxOy�У���A��x1��y1����B��x2��y2�����������x1+x2=0��y1��y2=0������x1��x2����Ƶ�A���B��Ϊ���ȵ㣮��֪����C��3��4��
��1�����и����У��� �����C��Ϊ���ȵ㣻
D����3����4����E��3��4����F����3��4��
��2����֪��G����5��4���������߶�CG�������߶�CG�ϴ�������P��Q��Ϊ���ȵ㣬���P�ĺ�����xP��ȡֵ��Χ��
��3����֪��O�İ뾶Ϊr������O�루2�����߶�CG���������㻥Ϊ���ȵ㣬��r��ȡֵ��Χ��
���𰸡�(1��F;(2) ��3��xP��3����xp��0;(3) 4��r��5.
����������������1�����ݻ�Ϊ���ȵ�����壬�ý��ۣ�
��2����Ϊ��P��Q���߶�CG�ϵĻ����ȵ㣬���ݣ�1���Ľ��ۣ���ȷ����P�ĺ�����xP��ȡֵ��Χ��
��3������Բ���߶�CG���롢���С��ཻ�������Ϊ���ȵ�Ķ��壬���۵ó�Բ�İ뾶��ȡֵ��Χ��
��⣺��1����Ϊ3+����3��=0��4��4=0
���Ե㣨��3��4����㣨3��4����Ϊ�෴�ȵ㣮
�ʴ�Ϊ����F��
��2�����ڵ�C���F��Ϊ���ȵ㣮
����Ϊ��P��Q���߶�CG�ϵķ��ȵ㣬
���Ե�P�ĺ�����xP��ȡֵ��ΧΪ����3��xP��3����xp��0��
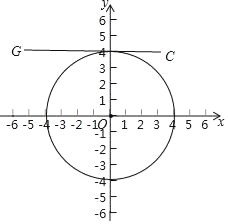
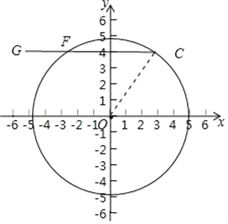
��3����ͼ��ʾ����
��O��CG����ʱ����ʱ��O���߶�CGû�л�Ϊ���ȵ㣻
����O��CG����ʱ����ʱr=4����O���߶�CGû�л�Ϊ���ȵ㣻
��O��CG�ཻ�ڵ�Cʱ����ʱr=![]() =5����O���߶�CG�л�Ϊ���ȵ㣻
=5����O���߶�CG�л�Ϊ���ȵ㣻
��r��4��ʱ����O���߶�CG��һ���������û�н��㣬
����û�л�Ϊ���ȵ㣮
���ϵ�4��r��5ʱ����O���߶�CG���������㣬���������㻥Ϊ���ȵ㣮

 ��������ϵ�д�
��������ϵ�д� ����˼ά����ѵ����ʱ��ѧ��ϵ�д�
����˼ά����ѵ����ʱ��ѧ��ϵ�д�