题目内容
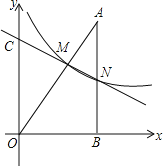
【题目】如图,在平面直角坐标系中,A点的坐标是(3,3),AB⊥x轴于点B,反比例函数y=![]() 的图象中的一支经过线段OA上一点M,交AB于点N,已知OM=2AM.
的图象中的一支经过线段OA上一点M,交AB于点N,已知OM=2AM.
(1)求反比例函数的解析式;
(2)若直线MN交y轴于点C,求△OMC的面积。
【答案】(1)y=![]() ;(2)
;(2)![]()
【解析】分析:(1)过点M作MH⊥x轴于点H.得出MH∥AB,那么△OMH∽△OAB,根据相似三角形对应边成比例求出点M的坐标,再利用待定系数法即可求出反比例函数的解析式;
(2)先由AB⊥x轴,A(3,4),得出N点横坐标为3.再把x=3代入y=![]() ,求出N点坐标,得到AN的值,根据OC∥AN,得出
,求出N点坐标,得到AN的值,根据OC∥AN,得出![]() =2,求出OC,然后根据△OMC的面积=
=2,求出OC,然后根据△OMC的面积=![]() OCOH,代入数值计算即可.
OCOH,代入数值计算即可.
详解:(1)过点M作MH⊥x轴于点H
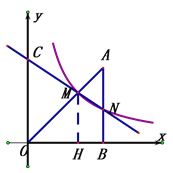
∵AB⊥x轴于点B
∴MH∥AB,
∴△OMH∽△OAB
∴![]()
∵A点的坐标是(3,3) OM=2AM
∴OB=3 AB=3 ![]()
∴OH=2 MH=2
∴M(2,2)
∵点N在反比例函数y=![]() 的图像上
的图像上
∴k=2×2=4
∴反比例函数的解析式为y=![]()
(2)∵AB⊥x轴 A(3,3)
∴N点的横坐标为3
把x=3代入y=![]() 得y=
得y=![]()
∴N点的坐标为(3,![]() )
)
∴AN=3-![]() =
=![]()
∵OC∥AN,
∴![]() =2,
=2,
∴OC=2AN=![]()
∴△OMC的面积:![]() OC·OH=
OC·OH=![]() ×
×![]() ×2=
×2=![]() .
.

练习册系列答案
 小学课时特训系列答案
小学课时特训系列答案
相关题目