题目内容
已知a、b、c是△ABC的三边长,且满足
+|a-b|=0,则△ABC的形状为( )
| c2-a2-b2 |
| A.等腰三角形 | B.直角三角形 |
| C.等腰直角三角形 | D.等边三角形 |
∵
+|a-b|=0,
∴c2-a2-b2=0,a-b=0,
解得:a2+b2=c2,a=b,
∴△ABC的形状为等腰直角三角形;
故选C.
| c2-a2-b2 |
∴c2-a2-b2=0,a-b=0,
解得:a2+b2=c2,a=b,
∴△ABC的形状为等腰直角三角形;
故选C.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
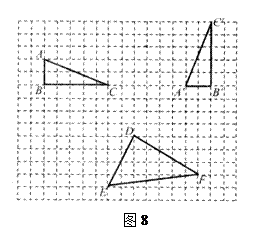
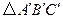 是由格点
是由格点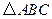 通过怎样变换得到的?
通过怎样变换得到的? 的坐标为(
的坐标为(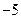 ,
,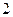 ),点
),点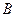 的坐标为
的坐标为 ,请求出过
,请求出过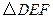 各顶点的坐标.
各顶点的坐标. 时,求菱形BNDM的面积.
时,求菱形BNDM的面积.


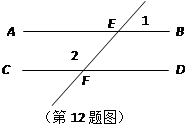
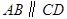 ,直线
,直线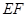 分别交
分别交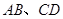 于点
于点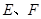 ,
,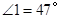 ,则
,则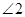 的大小是__________.
的大小是__________.