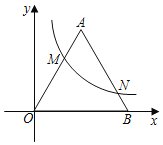题目内容
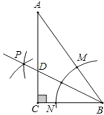
【题目】如图,在RtABC中,∠C=90°,以顶点B为圆心,适当长度为半径画弧,分别交AB,BC于点M,N,再分别以点M,N为圆心,大于![]() 的长为半径画弧,两弧交于点P,作射线BP交AC于点D.当∠A=30°时,小敏正确求得
的长为半径画弧,两弧交于点P,作射线BP交AC于点D.当∠A=30°时,小敏正确求得![]() :
:![]() =1:2.写出两条小敏求解中用到的数学依据:__________________.
=1:2.写出两条小敏求解中用到的数学依据:__________________.
【答案】答案不唯一,如直角三角形30度角所对直角边等于斜边的一半和等边对等角
【解析】
由已知条件得到![]() :
:![]() =1:2,写出其中的2条依据即可.
=1:2,写出其中的2条依据即可.
由作法得BD平分∠ABC,
∵∠C=90°,∠A=30°,
∴∠ABC=60°,(三角形的内角和为180)
∴∠ABD=∠CBD=30°(角平分线的性质),
∴DA=DB(等角对等边),
在Rt△BCD中,BD=2CD,(直角三角形30度角所对直角边等于斜边的一半)
∴AD=2CD(等量代换),
∴![]() :
:![]() =1:2.
=1:2.
故答案为:答案不唯一,如直角三角形30度角所对直角边等于斜边的一半和等边对等角.

练习册系列答案
相关题目
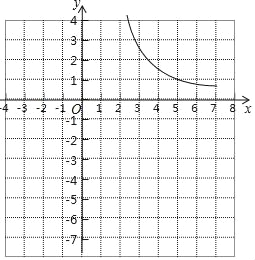
【题目】小邱同学根据学习函数的经验,研究函数y=![]() 的图象与性质.通过分析,该函数y与自变量x的几组对应值如下表,并画出了部分函数图象如图所示.
的图象与性质.通过分析,该函数y与自变量x的几组对应值如下表,并画出了部分函数图象如图所示.
x | 1 |
|
|
| 3 | 4 | 5 | 6 | … |
y | ﹣1 | ﹣2 | ﹣3.4 | ﹣7.5 | 2.4 | 1.4 | 1 | 0.8 | … |
(1)函数y=![]() 的自变量x的取值范围是 ;
的自变量x的取值范围是 ;
(2)在图中补全当1≤x<2的函数图象;
(3)观察图象,写出该函数的一条性质: ;
(4)若关于x的方程![]() =x+b有两个不相等的实数根,结合图象,可知实数b的取值范围是 .
=x+b有两个不相等的实数根,结合图象,可知实数b的取值范围是 .