题目内容
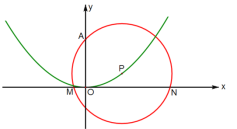
【题目】已知正比例函数![]() 的图象与反比例函数
的图象与反比例函数![]() (
(![]() 为常数,
为常数,![]() )的图象有一个交点的横坐标是2.
)的图象有一个交点的横坐标是2.
(1)求两个函数图象的交点坐标;
(2)若点![]() ,
,![]() 是反比例函数
是反比例函数![]() 图象上的两点,且
图象上的两点,且![]() ,试比较
,试比较![]() 的大小.
的大小.
【答案】(1)(2,2),(-2,-2);(2) 当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ;当
;当![]() 时,
时, ![]()
【解析】
(1)根据题意得出交点的纵坐标,然后求出k的值,从而得出函数解析式;(2)、根据函数的性质分三类情况进行讨论计算.
(1)由题意,得2k=![]() ,
,
解得k=1. ∴正比例函数的表达式为y=x,反比例函数的表达式为y=![]() .
.
解x=![]() ,得x=±2.由y=x,得y=±2. ∴两函数图象交点的坐标为(2,2),(-2,-2).
,得x=±2.由y=x,得y=±2. ∴两函数图象交点的坐标为(2,2),(-2,-2).
(2)∵反比例函数y=![]() 的图象分别在第一、三象限内, y的值随x值的增大而减小,
的图象分别在第一、三象限内, y的值随x值的增大而减小,
所以当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ;当
;当![]() 时,因为
时,因为![]() ,
,![]() ,
,![]()
∴综上所述:当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ;当
;当![]() 时,
时, ![]()

【题目】李辉到服装专卖店去做社会调查,了解到商店为了激励营业员的工作积极性实行了“月总收入=基本工资+计件奖金”的方法,并获得了如下信息:
营业员 | 嘉琪 | 嘉善 |
月销售件数/件 | 400 | 300 |
月总收入/元 | 7800 | 6600 |
假设月销售件数为x件,月总收入为y元,销售每件奖励a元,营业员月基本工资为b元.
(1)求a、b的值.
(2)若营业员嘉善某月总收入不低于4200元,那么嘉善当月至少要卖多少件衣服?
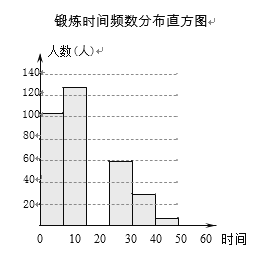
【题目】某数学活动小组为了解全县九年级学生在抗新冠病毒疫情期间平均每天居家锻炼时间,向全县部分学生进行了抽样调查,并将收集到的数据整理成如图的统计图(部分数据未标出).
(1)这次抽样调查的学生人数一共有 人;
(2)求频数分布表中 a 的值,并补全频数分布直方图; ,
(3)若该县有 5000 名九年级学生,请你估计全县九年级学生平均每天居家锻炼时间不超过20分钟的有多少人?
时间 x/分 | 人数/人 | 频率 |
0<x≤10 | 102 | 25.5% |
10<x≤20 | 132 | 33% |
20<x≤30 | a | 17.5% |
30<x≤40 | 59 | 14.75% |
40<x≤50 | 29 | 7.25% |
50<x≤60 | 8 | 2% |