题目内容
【题目】如图,已知点A是直线y=x与反比例函数y= ![]() (k>0,x>0)的交点,B是y=
(k>0,x>0)的交点,B是y= ![]() 图象上的另一点,BC//x轴,交y轴于点C.动点P从坐标原点O出发,沿O→A→B→C(图中“→”所示路线)匀速运动,终点为C,过点P作PM⊥x轴,PN⊥y轴,垂足分别为M,N.设四边形OMPN的面积为S,P点运动时间为t,则S关于t的函数图象大致为( )
图象上的另一点,BC//x轴,交y轴于点C.动点P从坐标原点O出发,沿O→A→B→C(图中“→”所示路线)匀速运动,终点为C,过点P作PM⊥x轴,PN⊥y轴,垂足分别为M,N.设四边形OMPN的面积为S,P点运动时间为t,则S关于t的函数图象大致为( )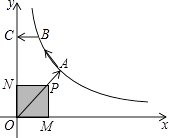
A.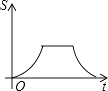
B.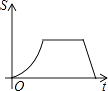
C.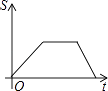
D.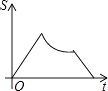
【答案】B
【解析】解:设点P的运动速度为v,
①由于点A在直线y=x上,
故点P在OA上时,四边形OMPN为正方形,
四边形OMPN的面积S= ![]() (vt)2 ,
(vt)2 ,
②点P在反比例函数图象AB时,
由反比例函数系数几何意义,四边形OMPN的面积S=k;
③点P在BC段时,设点P运动到点C的总路程为a,
则四边形OMPN的面积=OC(a﹣vt)=﹣OCvt+OCa,
纵观各选项,只有B选项图形符合.
故选:B.
【考点精析】关于本题考查的函数的图象,需要了解函数的图像是由直角坐标系中的一系列点组成;图像上每一点坐标(x,y)代表了函数的一对对应值,他的横坐标x表示自变量的某个值,纵坐标y表示与它对应的函数值才能得出正确答案.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目