题目内容

已知一个二次函数的图象为抛物线C，点P（1，-4）、Q（5，-4）、R（3，0）在抛物线C上．
（1）求这个二次函数的解析式．
（2）我们知道，与y=kx+b（即kx-y+b=0）可以表示直线一样，方程x+my+n=0也可以表示一条直线，且对于直线x+my+n=0和抛物线y=ax²+bx+c（a≠0），方程组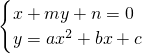 $数学公式$ 的解（x，y）作为点的坐标，所确定的点就是直线和抛物线的公共点，如果直线L：x+my+n=0过点M（1，0），且直线L与抛物线C有且只有一个公共点，求相应的m，n的值．

解：（1）y=-x²+6x-9．
（2）直线l为：x+my-1=0，
∵直线L与抛物线C有且只有一个公共点
∴ $\text{[math]}$ ，有且只有一解．
∴由x+my-1=0得x=1-my，（3）
把（3）代入二次函数中得：y=-（1-my）²+6（1-my）-9，
整理得：m²y²+（4m+1）y+4=0，
于是由△=（4m+1）²-4•m²•4=0，
∴m=- $\text{[math]}$ ，
故：当m=- $\text{[math]}$ ，n=-1时，直线l为：x+ $\text{[math]}$ y-1=0与抛物线C：y=-x²+6x-9有且只有一个公共点．
分析：（1）先设函数解析式为：y=ax²+bx+c，把三点的坐标值代入函数解析式，利用待定系数法可求出函数解析式．
（2）把（1，0）代入一次函数解析式，可先求出n的值，那么解有一次函数与二次函数组成的方程组，得到关于y的二次方程，因为只有一个交点，所以△=0，即可求出m的值．
点评：本题利用了待定系数法求函数解析式，以及解方程组，还有一元二次方程根的判别式等知识．