题目内容
 已知一个二次函数的图象经过A(0,1)、B(2,3)、C(-1,-
已知一个二次函数的图象经过A(0,1)、B(2,3)、C(-1,-| 3 | 2 |
(1)求这个二次函数的解析式;
(2)指出所求函数图象的顶点坐标和对称轴,并画出其大致图象.
分析:(1)二次函数y=x2+bx+c的图象经过点A,B,C,用待定系数法可得二次函数的解析式;
(2)运用顶点坐标公式求出其顶点坐标和对称轴,并根据解析式,结合二次函数的性质画出其大致图象.
(2)运用顶点坐标公式求出其顶点坐标和对称轴,并根据解析式,结合二次函数的性质画出其大致图象.
解答:解:(1)设所求二次函数解析式为y=ax2+bx+c(a≠0).
∵此二次函数的图象经过A(0,1)、B(2,3)、C(-1,-
)三点,
∴
,
解得
∴y=-
x2+2x+1;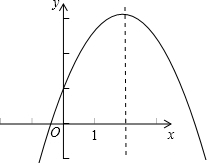
(2)∵y=-
x2+2x+1,
=2,
=3,
∴顶点坐标(2,3),对称轴:直线x=2.
正确画出图象
∵此二次函数的图象经过A(0,1)、B(2,3)、C(-1,-
| 3 |
| 2 |
∴
|
解得
|
∴y=-
| 1 |
| 2 |

(2)∵y=-
| 1 |
| 2 |
| -b |
| 2a |
| 4ac-b2 |
| 4a |
∴顶点坐标(2,3),对称轴:直线x=2.
正确画出图象
点评:本题主要考查了用待定系数法求函数的解析式及二次函数的顶点坐标和对称轴公式.

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目
 (2012•嘉定区一模)已知一个二次函数的图象经过A(0,3)、B(4,3)、C(1,0)三点(如图).
(2012•嘉定区一模)已知一个二次函数的图象经过A(0,3)、B(4,3)、C(1,0)三点(如图).