题目内容
 (2012•嘉定区一模)已知一个二次函数的图象经过A(0,3)、B(4,3)、C(1,0)三点(如图).
(2012•嘉定区一模)已知一个二次函数的图象经过A(0,3)、B(4,3)、C(1,0)三点(如图).(1)求这个二次函数的解析式;
(2)求tan∠BAC的值;
(3)若点D在x轴上,点E在(1)中所求出的二次函数的图象上,且以点A、C、D、E为顶点的四边形是平行四边形,求点D、E的坐标.
分析:(1)设二次函数解析式为y=ax2+bx+c,利用待定系数法列式计算出a、b、c的值,从而得解;
(2)过点C作CM⊥AB于点M,先求出点M的坐标,然后根据三角形函数的定义列式进行计算即可;
(3)根据抛物线的对称性结合平行四边形的性质可得AE∥x轴,从而得到点E与点B重合,然后根据平行四边形的对边相等求出CD的长度,再分点D在点C的左边与右边两种情况求解,从而得到点D的坐标.
(2)过点C作CM⊥AB于点M,先求出点M的坐标,然后根据三角形函数的定义列式进行计算即可;
(3)根据抛物线的对称性结合平行四边形的性质可得AE∥x轴,从而得到点E与点B重合,然后根据平行四边形的对边相等求出CD的长度,再分点D在点C的左边与右边两种情况求解,从而得到点D的坐标.
解答: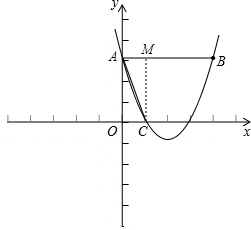 解:(1)设二次函数解析式为y=ax2+bx+c,
解:(1)设二次函数解析式为y=ax2+bx+c,
∴
,
解得
,
∴二次函数的解析式为y=x2-4x+3;
(2)如图,过点C作CM⊥AB于点M,
∴点M的坐标为(1,3),
tan∠BAC=
=
=3;
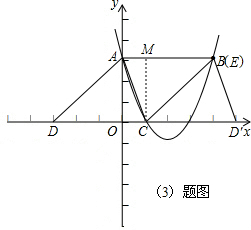
(3)∵点D在x轴上,点E在二次函数的图象上,
∴以点A、C、D、E为顶点的平行四边形中AE∥CD,
∴点E与点B重合,
∴点E的坐标为(4,3),
∴AE=4-0=4,
根据平行四边形的对边平行且相等CD=AE=4,
又∵点C的坐标为(1,0),
∴①当点D在点C的左边时,AC是对角线,1-4=-3,
点D的坐标为(-3,0),
②当点D在点C的右边时,AC是平行四边形的边,1+4=5,
点D的坐标为(5,0),
综上所述点D的坐标为(-3,0)或(5,0),点E的坐标为(4,3).
 解:(1)设二次函数解析式为y=ax2+bx+c,
解:(1)设二次函数解析式为y=ax2+bx+c,∴
|
解得
|
∴二次函数的解析式为y=x2-4x+3;
(2)如图,过点C作CM⊥AB于点M,
∴点M的坐标为(1,3),
tan∠BAC=
| CM |
| AM |
| 3 |
| 1 |

(3)∵点D在x轴上,点E在二次函数的图象上,
∴以点A、C、D、E为顶点的平行四边形中AE∥CD,
∴点E与点B重合,
∴点E的坐标为(4,3),
∴AE=4-0=4,
根据平行四边形的对边平行且相等CD=AE=4,
又∵点C的坐标为(1,0),
∴①当点D在点C的左边时,AC是对角线,1-4=-3,
点D的坐标为(-3,0),
②当点D在点C的右边时,AC是平行四边形的边,1+4=5,
点D的坐标为(5,0),
综上所述点D的坐标为(-3,0)或(5,0),点E的坐标为(4,3).
点评:本题是对二次函数的综合考查,包括待定系数法求二次函数解析式,锐角函数的三角函数,平行四边形的性质,在确定平行四边形的顶点时,判断出点E与点B重合是解题的关键.

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目
 (2012•嘉定区一模)如果二次函数y=ax2+bx+c的图象如图所示,那么下列判断中,正确的是( )
(2012•嘉定区一模)如果二次函数y=ax2+bx+c的图象如图所示,那么下列判断中,正确的是( ) (2012•嘉定区一模)如图,△ABC与△DEF的顶点均在方格纸中的小正方形方格(边长为一个单位长)的顶点处,则△ABC
(2012•嘉定区一模)如图,△ABC与△DEF的顶点均在方格纸中的小正方形方格(边长为一个单位长)的顶点处,则△ABC (2012•嘉定区一模)如图,已知平行四边形ABCD,点M是边BC的中点.设
(2012•嘉定区一模)如图,已知平行四边形ABCD,点M是边BC的中点.设