题目内容
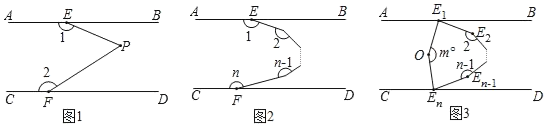
【题目】(提出问题)(1)如图1,已知AB∥CD,证明:∠1+∠EPF+∠2=360°;
(类比探究)(2)如图2,已知AB∥CD,设从E点出发的(n﹣1)条折线形成的n个角分别为∠1,∠2……∠n,探索∠1+∠2+∠3+……+∠n的度数可能在1700°至2000°之间吗?若有可能请求出n的值,若不可能请说明理由.
(拓展延伸)(3)如图3,已知AB∥CD,∠AE1E2的角平分线E1O与∠CEnEn﹣1的角平分线EnO交于点O,若∠E1OEn=m°.求∠2+∠3+∠4+…+∠(n﹣1)的度数.(用含m、n的代数式表示)
【答案】(1)见解析;(2)可能在1700°至2000°之间,n的值为11或12;(3)∠2+∠3+∠4+…+∠(n﹣1)=180°(n﹣1)﹣2m°.
【解析】
(1)过点P做PG∥AB,根据平行线的判定得出PG∥CD,根据平行线的性质得出结论即可;(2)过折点作AB的平行线,根据平行线的判定得出AB∥GH∥…∥PQ∥CD,根据平行线的性质得出即可;(3)过点O作OP∥AB,根据平行线的性质以及(2)中的结论,即可得出∠2+∠3+∠4+…∠(n-1)的度数.
(1)如图所示,过P作PG∥AB,则∠1+∠GPE=180°,
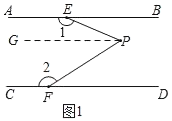
∵AB∥CD,
∴PG∥CD,
∴∠2+∠FPG=180°,
∴∠1+∠GPE+∠GPF+∠2=360°,
即∠1+∠EPF+∠2=360°;
(2)可能在1700°至2000°之间.
如图过G作GH∥AB,…,过P作PQ∥AB,
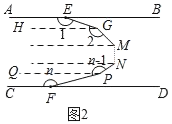
∵AB∥CD,
∴AB∥GH∥…∥PQ∥CD,
∴∠1+∠EGH=180°,…,∠QPF+∠n=180°,(有(n﹣1)对同旁内角)
∴∠1+∠2+…∠n﹣1+∠n=180°(n﹣1),
当1700°<180°(n﹣1)<2000°时,n=11,12,
∴n的值为11或12;
(3)如图所示,过O作OP∥AB,
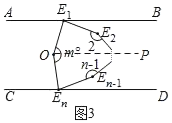
∵AB∥CD,
∴OP∥CD,
∴∠AE1O=∠POE1,∠CEnO=∠POEn,
∴∠AE1O+∠CEnO=∠POE1+∠POEn=∠E1OEn=m°,
又∵∠AE1E2的角平分线E1O与∠CEnEn﹣1的角平分线EnO交于点O,
∴∠AE1E2+∠CEnEn﹣1=2(∠AE1O+∠CEnO)=2m°,
由(2)可得,∠AE1E2+∠2+…+∠(n﹣1)+∠CEnEn﹣1=180°(n﹣1),
∴∠2+∠3+∠4+…+∠(n﹣1)=180°(n﹣1)﹣2m°.

 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案【题目】为了了解七年级学生体育测试成绩情况,现从中随机抽取部分学生的体育成绩统计如下,其中右侧扇形统计图中的圆心角α为36°,根据图表中提供的信息,回答下列问题:
体育成绩统计表 | ||
体育成绩(分) | 人数(人) | 百分比(%) |
26 | 8 | 16 |
27 | 12 | 24 |
28 | 15 | |
29 | n | |
30 | ||
(1)求样本容量及n的值;
(2)已知该校七年级共有500名学生,如果体育成绩达28分以上为优秀,请估计该校七年级学生体育成绩达到优秀的总人数.