题目内容
【题目】某商店经销一种成本为每千克40元的水产品，据市场分析，若按每千克50元销售，一个月能售出500千克．若销售价每涨1元，则月销售量减少10千克．
（1）要使月销售利润达到最大，销售单价应定为多少元？
（2）要使月销售利润不低于8000元，请结合图象说明销售单价应如何定？
【答案】（1）70元；（2）周销售利润不低于8000元．
【解析】试题分析：（1）月销售利润=每千克的利润×可卖出千克数，把相关数值代入，然后利用配方法即可得；
（2）根据题意画出图象，通过观察即可得.
试题解析：（1）设销售单价定为每千克x元，获得利润为w元，则：
w=（x﹣40）[500﹣（x﹣50）×10]，
=﹣10x2+1400x﹣40000，
=﹣10（x﹣70）2+9000，
故当x=70时，利润最大为9000元．
答：要使月销售利润达到最大，销售单价应定为70元；
（2）令y=8000，则﹣10（x﹣20）2+9000=8000，
解得x1=10，x2=30．
函数的大致图象为：
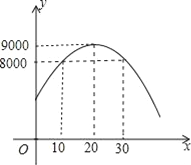
观察图象当10≤x≤30时，y不低于8000．
所以当销售单价不小于10元而不大于30元时，商场获得的周销售利润不低于8000元．
阅读快车系列答案
【题目】（本题满分10分）科幻小说《实验室的故事》中，有这样一个情节，科学家把一种珍奇的植物分别放在不同温度的环境中，经过一天后，测试出这种植物高度的增长情况（如下表）：
温度 | …… | －4 | －2 | 0 | 2 | 4 | 4.5 | …… |
植物每天高度增长量 | …… | 41 | 49 | 49 | 41 | 25 | 19.75 | …… |
由这些数据，科学家推测出植物每天高度增长量
是温度
的函数，且这种函数是反比例函数、一次函数和二次函数中的一种．
（1）请你选择一种适当的函数，求出它的函数关系式，并简要说明不选择另外两种函数的理由；
（2）温度为多少时，这种植物每天高度的增长量最大？
（3）如果实验室温度保持不变，在10天内要使该植物高度增长量的总和超过250mm，那么实验室的温度应该在哪个范围内选择？请直接写出结果．
