题目内容
【题目】如图1，AD和AE分别是△ABC的BC边上的高和中线，点D是垂足，点E是BC的中点，规定：λA= 
．特别地，当点D、E重合时，规定：λA=0．另外，对λB、λC作类似的规定．
（1）如图2，在△ABC中，∠C=90°，∠A=30°，求λA、λC；
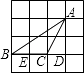
（2）在每个小正方形边长均为1的4×4的方格纸上，画一个△ABC，使其顶点在格点（格点即每个小正方形的顶点）上，且λA=2，面积也为2；
（3）判断下列三个命题的真假（真命题打“√”，假命题打“×”）：
①若△ABC中λA＜1，则△ABC为锐角三角形；
②若△ABC中λA=1，则△ABC为直角三角形；
③若△ABC中λA＞1，则△ABC为钝角三角形． ．
【答案】
（1）
解：如图，
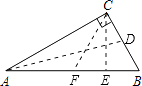
作BC边上的中线AD，又AC⊥DC，
∴λA= 
=1，
过点C分别作AB边上的高CE和中线CF，
∵∠ACB=90°，
∴AF=CF，
∴∠ACF=∠CAF=30°，
∴∠CFE=60°，
∴λC= 
=cos60°= 
（2）
解：如图：
（3）解：×；√；√
【解析】解： （3）①在第（1）题中，λC= ，而△ABC是直角三角形，故命题错误；②λA=1时，过顶点A的高线的垂足与三角形的顶点一定重合，故三角新一定是直角三角形，故命题正确；③λA＞1时，过顶点A的高线的垂足与三角形的顶点一定在边的延长线上，则三角形一定是钝角三角形，故命题正确．
所以答案是：①×，②√，③√．
【考点精析】本题主要考查了三角形的“三线”和解直角三角形的相关知识点，需要掌握1、三角形角平分线的三条角平分线交于一点(交点在三角形内部，是三角形内切圆的圆心，称为内心);2、三角形中线的三条中线线交于一点(交点在三角形内部，是三角形的几何中心，称为中心);3、三角形的高线是顶点到对边的距离；注意：三角形的中线和角平分线都在三角形内；解直角三角形的依据：①边的关系a2+b2=c2；②角的关系：A+B=90°；③边角关系：三角函数的定义．(注意：尽量避免使用中间数据和除法)才能正确解答此题．
