��Ŀ����
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���O������ԭ�㣬��B��0��12������A�ڵ�һ�����ڣ���AOBΪ���������Σ���BAO=90�㣬AB=AO��AC��OB����D�ӵ�B��������ÿ��2����λ���ٶ���y�����յ�O�˶�������DA������A��AE��AD������AE��x���ڵ�E������BE�����߶�AC�ڵ�F�����߶�OA�ڵ�G��
��1����ֱ��д��A�����ꣻ
��2����D�˶���ʱ��Ϊt��ʱ���ú�t�Ĵ���ʽ��ʾ��ACD�����S����д��t��ȡֵ��Χ��
��3���ڣ�2���������£����ı���DAEO���������6Sʱ������AGF�������
��
���𰸡���1��A��6��6������2������D���߶�BC��ʱ����������C��������0��t��3��S= 18��6t������D���߶�BC��ʱ����������C��������3��t��6����S= 6t��18����3��������D���߶�BC��ʱ����������C��������0��t��3��S��AFG=6��������D���߶�OC�ϣ���������C��������3��t��6��S��AFG=![]() ��
��
��������
��1����ȷ����OB=12�����õ���ֱ�������ε����ʵ�AC=BC=OC=![]() OB=6�����ɵó����ۣ�
OB=6�����ɵó����ۣ�
��2������D���߶�BC��ʱ����������C��������0��t��3���ó�CD=BC-BD=6-2t�����������������ʽ���ɣ�
����D���߶�BC��ʱ����������C��������3��t��6����ͼ2��CD=BD-BC=2t-6��������������������ʽ���ɣ�
��3���ٵ���D���߶�BC��ʱ����������C��������0��t��3����ͼ1�����жϳ�S��ACD=S��AME������S�ı���DOEA=S������ACOM=AC2=36���������S������t=2��CD=EM=2��OE=4�������AF=AC-CF=4=OE������жϳ���AFG�ա�OEG�����PG=QG=6���ɵó����ۣ�
�ڵ���D���߶�OC�ϣ���������C��������3��t��6����ͼ2��ͬ�ٵķ���֪��S=6��t=4��CD=EM=2��OE=8��ͬ�ٵķ����ã�OF=4����AF=AC-OF=2�����жϳ���AFG�ס�OEG���ó�h'=4h�����ɵó�h=![]() ���ɵó����ۣ�
���ɵó����ۣ�
��1����B��0��12����
��OB=12��
�ߡ�AOBΪ���������Σ���BAO=90�㣬AB=AO��AC��OB��
��AC=BC=OC=![]() OB=6��
OB=6��
��A��6��6����
��2������D���߶�BC��ʱ����������C��������0��t��3����ͼ1��
���˶�֪��BD=2t��
��CD=BC��BD=6��2t��
��S=S��ACD=![]() CD��AC=18��6t��
CD��AC=18��6t��
����D���߶�BC��ʱ����������C��������3��t��6����ͼ2��
���˶�֪��BD=2t��
��CD=BD��BC=2t��6��
��S=S��ACD=![]() CD��AC=6t��18��
CD��AC=6t��18��
��3���ٵ���D���߶�BC��ʱ����������C��������0��t��3����ͼ1��
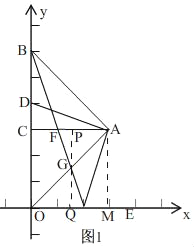
����A��AM��x����M��
���ı���OCAM�Ǿ��Σ�
��A��6��6����
��AC=AM��
�����OCAM��������
��OM=AC=6����CAM=90�㣬
�ߡ�DAE=90�㣬
���CAD=��EAM��
����ACD����AME��
 ��
��
���ACD�ա�AME��
��S��ACD=S��AME��
��S�ı���DOEA=S��ACD+S�ı���COEA=S��AMF+S�ı���COEA=S������ACOM=AC2=36��
���ı���DAEO���������6S��
��6S=36��
��S=6��
�ɣ�2��֪��S=18��6t��
��18��6t=6��
��t=2��
��CD=EM=6��2t=2��
��OM=6��
��OE=OM��EM=4��
��AC��OM��OC=BC��
��CF=![]() OE=2��
OE=2��
��AF=AC��CF=4=OE��
����G��GQ��OM��Q����AC��P��
��PG��AC��
���ı���OCPQ�Ǿ��Σ�
��PQ=OC=6��
��֪����AFG�ա�OEG��
��PG=QG=6��
��S��AFG=![]() AF��PG=6��
AF��PG=6��
�ڵ���D���߶�OC�ϣ���������C��������3��t��6����ͼ2��

ͬ�ٵķ���֪��S=6��
��S=6t��18��
��6t��18=6��
��t=4��
��CD=EM=2��
��OE=8��
ͬ�ٵķ����ã�OF=4��
��AF=AC��OF=2��
��AC��OM��
���AFG�ס�OEG��
����AFG�ı�AF�ϵĸ�Ϊh����OEG�ı�OE�ϵĸ�Ϊh'��
��![]() ��
��
��h'=4h��
��h+h'=6��
��h=![]() ��
��
��S��AFG=![]() AF��h=
AF��h=![]() ��
��