题目内容
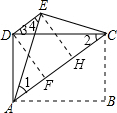
如图，四边形ABCD是矩形，AD=3，AB=4，把矩形沿直线AC折叠，点B落在点E处，连接DE，则DE的长为（ ）
| A．1 | B．
| C．
| D．
|
过D作DF⊥AC于F，过E作EH⊥AC于H，如图，
∵四边形ABCD为矩形，
∴Rt△ABC≌Rt△CDA，
又∵矩形沿着直线AC折叠，使点B落在点E处，
∴Rt△ABC≌Rt△AEC，
∴△ADC≌△CEA，
∴CE=AD，
根据全等三角形的面积相等，得：DF=EH，
∵EH∥DF，
∴四边形DFHE是平行四边形，
∴DE∥AC，
∵AD=CE，
∴四边形DACE是等腰梯形，
S△ADC=
AD×DC=
AC×DF，
∵AD=3，DC=4，由勾股定理得：AC=5，
∴DF=
=EH，
在△ADF中，由勾股定理得：AF=CH=
=
，
∴DE=FH=5-2×
=
．
故选D．
∵四边形ABCD为矩形，
∴Rt△ABC≌Rt△CDA，
又∵矩形沿着直线AC折叠，使点B落在点E处，
∴Rt△ABC≌Rt△AEC，
∴△ADC≌△CEA，
∴CE=AD，
根据全等三角形的面积相等，得：DF=EH，
∵EH∥DF，
∴四边形DFHE是平行四边形，
∴DE∥AC，
∵AD=CE，
∴四边形DACE是等腰梯形，
S△ADC=
| 1 |
| 2 |
| 1 |
| 2 |
∵AD=3，DC=4，由勾股定理得：AC=5，
∴DF=
| 12 |
| 5 |
在△ADF中，由勾股定理得：AF=CH=
32-(
|
| 9 |
| 5 |
∴DE=FH=5-2×
| 9 |
| 5 |
| 7 |
| 5 |
故选D．
练习册系列答案
双基同步导航训练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
