题目内容
【题目】如图,在Rt△ABC中,∠ACB=90°,BC=30cm,AC=40cm,点D在线段AB上,从点B出发,以2cm/s的速度向终点A运动,设点D的运动时间为t秒。

(1)点D在运动t秒后,BD= cm(用含有t的式子表示)
(2)AB=cm,AB边上的高为cm;
(3)点D在运动过程中,当△BCD为等腰三角形时,求t的值.
【答案】(1)![]() ;(2)50;24;(3)t的值为15s或18s或12.5s.
;(2)50;24;(3)t的值为15s或18s或12.5s.
【解析】
(1)根据点D以2cm/s的速度向终点A运动,设点D的运动时间为t秒,即可表示出![]() ;
;
(2)利用勾股定理求出AB的长,再利用三角形面积公式即可求得AB边上的高;
(3)分三种情况:①当BD=BC=30cm时得到2t=30,即可得到结果;
②当CD=CB=30cm时,作CE⊥AB于E,则![]() ,由(1)得CE=24,由勾股定理求出BE,即可得出结果;
,由(1)得CE=24,由勾股定理求出BE,即可得出结果;
③当DB=DC时,∠BCD=∠B,证明DA=DC,得出AD=DB=![]() AB,即可得出结果.
AB,即可得出结果.
(1) ∵点D以2cm/s的速度向终点A运动,设点D的运动时间为t秒
∴![]()
故答案为:![]()
(2)由勾股定理得,![]()
设AB边上的高为h,![]()
∴![]() ,
,
解得:![]()
故答案为:50;24.
(3) 分三种情况:
①当BD=BC=30cm时,2t=30
∴t=15(s)
②当CD=CB=30cm时,作CE⊥AB于E,如图所示:
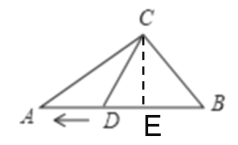
则![]()
由(2)得,AB边上的高CE=24,
在![]() 中,由勾股定理得:
中,由勾股定理得:
![]()
∴![]()
③当DB=DC时,∠BCD=∠B
∵∠A=90°﹣∠B,∠ACD=90°﹣∠BCD,
∴∠ACD=∠A
∴DA=DC
∴AD=DB=![]() AB=25(cm)
AB=25(cm)
∴![]()
![]()
综上所述,t的值为15s或18s或12.5s.

练习册系列答案
相关题目