题目内容
【题目】给出如下定义:对于⊙O 的弦 MN 和⊙O 外一点 P(M,O,N 三点不共线,且点 P,O 在直线 MN 的异侧),当∠MPN+∠MON=180°时,则称点 P 是线段 MN 关于点 O 的关联点.图 1 是点 P 为线段 MN 关于点 O 的关联点的示意图.
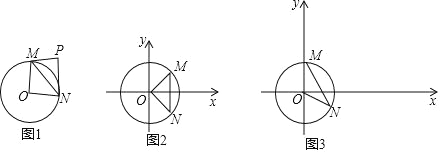
在平面直角坐标系 xOy 中,⊙O 的半径为 1.
(1)如图 2,已知 M(![]() ,
,![]() ),N(
),N( ![]() ,﹣
,﹣![]() ),在 A(1,0),B(1,1),C(
),在 A(1,0),B(1,1),C(![]() ,0)三点中,是线段 MN 关于点 O 的关联点的是哪个点;
,0)三点中,是线段 MN 关于点 O 的关联点的是哪个点;
(2)如图 3,M(0,1),N(![]() ,﹣
,﹣![]() ),点 D 是线段 MN 关于点 O 的关联点.
),点 D 是线段 MN 关于点 O 的关联点.
①求∠MDN 的大小;
②在第一象限内有一点 E(![]() m,m),点 E 是线段 MN 关于点 O 的关联点,判断△MNE 的形状,并直接写出点 E 的坐标;
m,m),点 E 是线段 MN 关于点 O 的关联点,判断△MNE 的形状,并直接写出点 E 的坐标;
③点 F 在直线 y=﹣![]() x+2 上,当∠MFN≥∠MDN 时,求点 F 的横坐标 x 的取值范围.
x+2 上,当∠MFN≥∠MDN 时,求点 F 的横坐标 x 的取值范围.
【答案】(1)点 C 满足条件;(2)①60°;②△MNE 是等边三角形;③满足条件的点 F 的横坐标 x 的取值范围![]() ≤xF≤
≤xF≤![]() .
.
【解析】
(1)由题意线段 MN 关于点O的关联点的是以线段 MN 的中点为圆心,![]() 为半径的圆上,所以点 C 满足条件;(2)①如图 3﹣1 中,作 NH⊥x 轴于 H.易求∠MON 的度数,再根据“关联点”的定义即可求得∠MDN 的大小;②如图 3﹣2 中,结论:△MNE 是等边三角形.作 EK⊥x 轴于 K,求得∠MOE=60°;由∠MON+∠MEN=180°,推出 M、O、N、E 四点共圆,可得∠MNE=∠MOE=60°,由此即可解决问题;③如图 3﹣3 中,由②可知,△MNE 是等边三角形,作△MNE 的外接圆⊙O′,首先证明点 E 在直线 y=﹣
为半径的圆上,所以点 C 满足条件;(2)①如图 3﹣1 中,作 NH⊥x 轴于 H.易求∠MON 的度数,再根据“关联点”的定义即可求得∠MDN 的大小;②如图 3﹣2 中,结论:△MNE 是等边三角形.作 EK⊥x 轴于 K,求得∠MOE=60°;由∠MON+∠MEN=180°,推出 M、O、N、E 四点共圆,可得∠MNE=∠MOE=60°,由此即可解决问题;③如图 3﹣3 中,由②可知,△MNE 是等边三角形,作△MNE 的外接圆⊙O′,首先证明点 E 在直线 y=﹣![]() x+2 上,设直线交⊙O′于 E、F,可得 F(
x+2 上,设直线交⊙O′于 E、F,可得 F(![]() ,
, ![]() ),观察图形即可解决问题.
),观察图形即可解决问题.
(1)由题意线段 MN 关于点 O 的关联点的是以线段 MN 的中点为圆心,![]() 为半径的圆上,所以点 C 满足条件;
为半径的圆上,所以点 C 满足条件;
(2)①如图 3﹣1 中,作 NH⊥x 轴于 H.
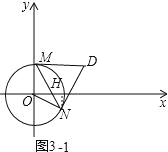
∵N(![]() ,﹣
,﹣![]() ),
),
∴tan∠NOH=![]() ,
,
∴∠NOH=30°,
∠MON=90°+30°=120°,
∵点 D 是线段 MN 关于点 O 的关联点,
∴∠MDN+∠MON=180°,
∴∠MDN=60°.
②如图 3﹣2 中,
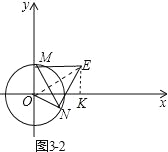
结论:△MNE 是等边三角形.
理由:作 EK⊥x 轴于 K.
∵E(![]() m,m),
m,m),
∴tan∠EOK=![]() ,
,
∴∠EOK=30°,
∴∠MOE=60°,
∵∠MON+∠MEN=180°,
∴M、O、N、E 四点共圆,
∴∠MNE=∠MOE=60°,
∵∠MEN=60°,
∴∠MEN=∠MNE=∠NME=60°,
∴△MNE 是等边三角形.
③如图 3﹣3 中,由②可知,△MNE 是等边三角形,作△MNE 的外接圆⊙O′,
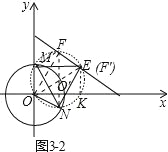
易知 E(![]() ,1),
,1),
∴点 E 在直线 y=﹣![]() x+2 上,设直线交⊙O′于 E、F,可得 F(
x+2 上,设直线交⊙O′于 E、F,可得 F(![]() ,
,![]() ),
),
观察图象可知满足条件的点F的横坐标 x 的取值范围![]() ≤xF≤
≤xF≤![]() .
.

 阅读快车系列答案
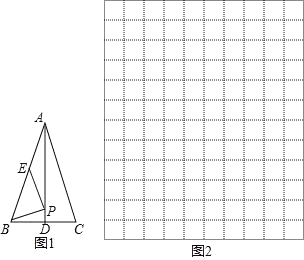
阅读快车系列答案【题目】如图 1,在等腰△ABC 中,AB=AC,点 D,E 分别为 BC,AB 的中点,连接 AD.在线段 AD 上任取一点 P,连接 PB,PE.若 BC=4,AD=6,设 PD=x(当点 P 与点 D 重合时,x 的值为 0),PB+PE=y.
小明根据学习函数的经验,对函数y 随自变量x 的变化而变化的规律进行了探究. 下面是小明的探究过程,请补充完整:
(1)通过取点、画图、计算,得到了 x 与 y 的几组值,如下表:
x | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
y | 5.2 | 4.2 | 4.6 | 5.9 | 7.6 | 9.5 |
说明:补全表格时,相关数值保留一位小数.(参考数据:![]() ≈1.414,
≈1.414,![]() ≈1.732,
≈1.732,![]() ≈2.236)
≈2.236)
(2)建立平面直角坐标系(图 2),描出以补全后的表中各对对应值为坐标的点,画出该函数的图象;
(3)求函数 y 的最小值(保留一位小数),此时点 P 在图 1 中的什么位置.