题目内容
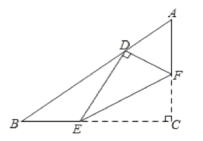
【题目】已知BD为正方形ABCD的对角线,P、Q两点分别在AB、BD上,且满足∠PCQ=∠ABD.
(1)求:![]() 的值;
的值;
(2)由于四边形不具稳定性,把正方形ABCD沿D向右拉动,使∠BAD=120时,此时线段CD、DQ、BP有何数量关系,请说明理由.
(3)如图3,在(2)的条件下,延长CQ交AD边于点E交BA的延长线于点M,作∠DCE的平分线交AD边于点F,若CQ:PM=5:7,EF= a,求线段CD的长.

【答案】(1)![]() ;(2)
;(2)![]() DQ+BP=2CD,理由见解析;(3)DC=
DQ+BP=2CD,理由见解析;(3)DC=![]() .
.
【解析】
(1)连接AC,由题意知:∠PCQ=∠ABD=45°,由于∠ACD=45°,故∠PCA=∠QCD,又∠CDQ=∠PAC,故△APC∽△DQC.相似三角形对应边成比例,即能得出本题结果.
(2) 作∠QCK=∠PCQ,过B作BL∥CK,连接AC, 得∠CQD=∠CKD.BL∥CK,则∠BLD∠CQD,∠BDL=∠CDB,则△BLD∽△CQD,知![]() =
=![]() =
=![]() ,则DL=
,则DL=![]() DQ,CD+DK=
DQ,CD+DK=![]() DQ,又通过证明△ACP≌DCK,故DK=AP,所以CD+DK=CD+AP=2CD-BP=
DQ,又通过证明△ACP≌DCK,故DK=AP,所以CD+DK=CD+AP=2CD-BP=![]() DQ.
DQ.
(3)根据题意易得:∠BDC=∠PCQ=30°,∠PMC=∠QCD,则△DQC∽△MPC,所以![]() =
=![]() =5:7,设BC=5k,MC=7k,过C作CG
=5:7,设BC=5k,MC=7k,过C作CG![]() AB与G,则CGB=90°.AD∥BC易得∠ABC=60°,所以BG=
AB与G,则CGB=90°.AD∥BC易得∠ABC=60°,所以BG=![]() k,CG=
k,CG=![]() k,在Rt△MGC中,根据勾股定理知MG=
k,在Rt△MGC中,根据勾股定理知MG=![]() k,则BM=8k,AB=BC=5k,AM=3k,因为AM∥CD易知△AME∽△DCE,则知AE=
k,则BM=8k,AB=BC=5k,AM=3k,因为AM∥CD易知△AME∽△DCE,则知AE=![]() k,延长CF、BM交于H,易得∠MCH=MHC,则,MH=MC=7k,AH=10k. △DFC∽△AFH,知
k,延长CF、BM交于H,易得∠MCH=MHC,则,MH=MC=7k,AH=10k. △DFC∽△AFH,知![]() =
=![]() =1:2,易知AF=
=1:2,易知AF=![]() k,又EF=a,则k=
k,又EF=a,则k=![]() a,所以DC=
a,所以DC=![]() a。
a。
(1)如图1,连接AC,四边形ABCD是正方形.
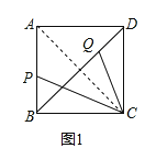
∴∠PCQ=∠CDQ=45°,∠PAC=∠QDC=∠ACD=45°
∴∠ACP+∠ACQ=∠ACQ+∠QCD=45°.
∴∠ACP=∠QCD,
∴△APC∽△DQC.
∴![]() .
.
(2)猜想:![]() DQ+BP=2CD
DQ+BP=2CD
理由如下:如图2,作∠QCK=∠PCQ,过B作BL∥CK,连接AC.
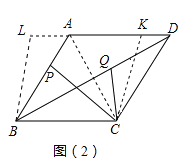
由题得四边形ABCD为菱形,∠BAD=120°,
∴∠ABD=∠ADB=30°,
∵∠QCK=∠ADB,
∴∠CQD=∠CKD
∵CK∥BL,
∴∠CKD=∠BLD,
∴△DLB∽△DQC.
∴![]()
∴DL=![]() DQ,
DQ,
∴CD+DK=![]() DQ,
DQ,
∵∠BAD=120,∠PCK=60 AC平分∠PAK,
∴∠APC=∠CKD ∠PAC=∠KDC DC=AC
∴△ACP≌△DCK,
∴DK=AP,
∴CD+DK=CD+AP=2CDBP=![]() DQ,
DQ,
即![]() DQ+BP=2CD;
DQ+BP=2CD;
(3)在菱形ABCD中,∠ABD=∠BDC=30°,
∴∠PCQ=∠CDQ=∠PCQ=∠ABD=30°,.
∵BM∥CD,
∴∠PMC=∠DCQ,
∴△DQC∽△MPC
∴CQ:PM=DC:MC=5:7,
∴BC:MC=5:7.
设BC=5k,则MC=7k,如图3,过C作CG⊥AB于G,则∠CGB=90°
∵AD∥BC,
∴∠BAD+∠ABC=180°.
∵∠BAD=120°.
∴∠ABC=60°.
∴BG=![]() k,CG=
k,CG=![]() .
.
在Rt△MGC中,MG=![]() =
=![]() k,
k,
∴BM=8k.
∵AB=BC=5k,
∴AM=BMAB=3k.
∵AM∥CD,
∴∠AMC=∠DCM,
∵∠AEM=∠DEC,
∴△AME∽△DCE,
∴AM:DC=AE:DE.
∴AE=![]() k.
k.
延长CF、BM交于H,
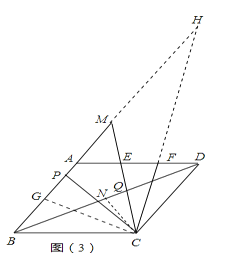
则∠DCF=∠MHC
∵FC平分∠ECD,
∴∠ECF=∠DCF,
∴∠MCH=∠MHC,
∴MH=MC=7k,
∴AH=AM+MH=10k.
∵∠HFA=∠CFD,
∴△DFC∽△AFH,
∴DF:AF=DC:AH=1:2
∴AF=![]() k, EF=AFAE=
k, EF=AFAE=![]() k,
k,
∵EF=![]() k=
k=![]() ,
,
∴k=![]()
∴DC=![]() .
.

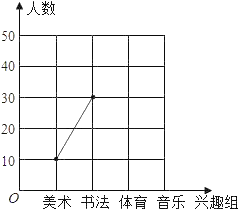
【题目】某校计划开设美术、书法、体育、音乐兴趣班,为了解学生报名的意向,随机调查了部分学生,要求被调查的学生必选且只选一项,根据调查结果绘制出如下不完整的统计图表:
兴趣班 | 人数 | 百分比 |
美术 | 10 |
|
书法 | 30 |
|
体育 |
|
|
音乐 | 20 |
|
根据统计图表的信息,解答下列问题:
(1)直接写出本次调查的样本容量和表中![]() 的值;
的值;
(2)将折线图补充完整;
(3)该校现有2000名学生,估计该校参加音乐兴趣班的学生有多少人?