题目内容
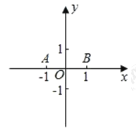
【题目】在平面直角坐标系xOy中(如图),已知抛物线y=x2-2x,其顶点为A.
(1)写出这条抛物线的开口方向、顶点A的坐标,并说明它的变化情况;
(2)我们把一条抛物线上横坐标与纵坐标相等的点叫做这条抛物线的“不动点”
①试求抛物线y=x2-2x的“不动点”的坐标;
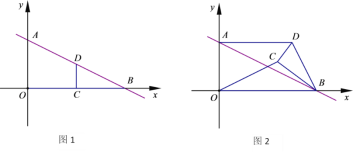
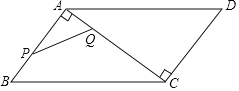
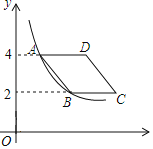
②平移抛物线y=x2-2x,使所得新抛物线的顶点B是该抛物线的“不动点”,其对称轴与x轴交于点C,且四边形OABC是梯形,求新抛物线的表达式.
【答案】(l)抛物线y=x2-2x的开口向上,顶点A的坐标是(1,-1),抛物线的变化情况是:抛物线在对称轴左侧的部分是下降的,右侧的部分是上升的;(2)①(0,0)、(3,3); ②新抛物线的表达式是y=(x+1)2-1.
【解析】
(1)![]()
![]() ,故该抛物线开口向上,顶点
,故该抛物线开口向上,顶点![]() 的坐标为
的坐标为![]() ;
;
(2)①设抛物线“不动点”坐标为![]() ,则
,则![]() ,即可求解;②新抛物线顶点
,即可求解;②新抛物线顶点![]() 为“不动点”,则设点
为“不动点”,则设点![]() ,则新抛物线的对称轴为:
,则新抛物线的对称轴为:![]() ,与
,与![]() 轴的交点
轴的交点![]() ,四边形
,四边形![]() 是梯形,则直线
是梯形,则直线![]() 在
在![]() 轴左侧,而点
轴左侧,而点![]() ,点
,点![]() ,则
,则![]() ,即可求解.
,即可求解.
(l)![]()
![]() ,
,
抛物线y=x2-2x的开口向上,顶点A的坐标是(1,-1),
抛物线的变化情况是:抛物线在对称轴左侧的部分是下降的,右侧的部分是上升的.
(2)①设抛物线y=x2-2x的“不动点”坐标为(t,t).
则t=t2-2t,解得t1=0,t2=3.
所以,抛物线y=x2-2x的“不动点”的坐标是(0,0)、(3,3).
②∵新抛物线的顶点B是其“不动点”,∴设点B的坐标为(m,m)
∴新抛物线的对称轴为直线x=m,与x轴的交点为C(m,0)
∵四边形OABC是梯形,
∴直线x=m在y轴左侧.
∵BC与OA不平行
∴OC∥AB.
又∵点A的坐标为(1,一1),点B的坐标为(m,m),
![]() m=-1.
m=-1.
∴新抛物线是由抛物线y=x2-2x向左平移2个单位得到的,
∴新抛物线的表达式是y=(x+1)2-1.

 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案