题目内容
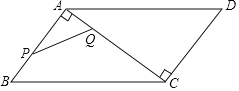
【题目】如图,某海监船以60海里/时的速度从A处出发沿正西方向巡逻,一可疑船只在A的西北方向的C处,海监船航行1.5小时到达B处时接到报警,需巡査此可疑船只,此时可疑船只仍在B的北偏西![]() 方向的C处,然后,可疑船只以一定速度向正西方向逃离,海监船立刻加速以90海里/时的速度追击,在D处海监船追到可疑船只,D在B的北偏西
方向的C处,然后,可疑船只以一定速度向正西方向逃离,海监船立刻加速以90海里/时的速度追击,在D处海监船追到可疑船只,D在B的北偏西![]() 方同.(以下结果保留根号)
方同.(以下结果保留根号)
(1)求B,C两处之问的距离;
(2)求海监船追到可疑船只所用的时间.

【答案】(1)B,C两处之问的距离为![]() 海里;(2)海监船追到可疑船只所用的时间为
海里;(2)海监船追到可疑船只所用的时间为![]() 小时.
小时.
【解析】
(1)作CE⊥AB于E,则∠CEA=90°,由题意得:AB=60×1.5=90,∠CAB=45°,∠CBN=30°,∠DBN=60°,得出△ACE是等腰直角三角形,∠CBE=60°,得出CE=AE,∠BCE=30°,由直角三角形的性质得出CE=![]() BE,BC=2BE,设BE=x,则CE=
BE,BC=2BE,设BE=x,则CE=![]() x,AE=BE+AB=x+90,得出方程
x,AE=BE+AB=x+90,得出方程![]() x=x+90,解得:x=45
x=x+90,解得:x=45![]() +45,得出BC=2x=90
+45,得出BC=2x=90![]() +90即可;
+90即可;
(2)作DF⊥AB于F,则DF=CE=![]() x=135+45
x=135+45![]() ,∠DBF=30°,由直角三角形的性质得出BD=2DF=270+90
,∠DBF=30°,由直角三角形的性质得出BD=2DF=270+90![]() ,即可得出结果.
,即可得出结果.
(1)作![]() 于E,如图1所示:则
于E,如图1所示:则![]() ,
,
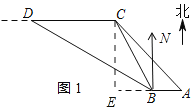
由题意得:![]() (海里),
(海里),![]() ,
,![]() ,
,![]() ,
,
∴![]() 是等腰直角三角形,
是等腰直角三角形,![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
设![]() ,则
,则![]() ,
,![]() ,
,
∴![]() ,
,
解得:![]() ,
,
∴![]() ;
;
答:B,C两处之问的距离为![]() 海里;
海里;
(2)作![]() 于F,如图2所示:
于F,如图2所示:
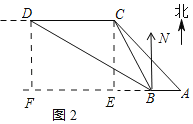
则![]() ,
,![]() ,
,
∴![]() ,
,
∴海监船追到可疑船只所用的时间为![]() (小时);
(小时);
答:海监船追到可疑船只所用的时间为![]() 小时.
小时.

练习册系列答案
相关题目