题目内容
【题目】今年4月某小学五年级一班同学积极参加了植树活动，临走时同学们都对自己植树区域做了标记。6月份该班同学绘制出植树区域树苗成活情况的部分统计图。
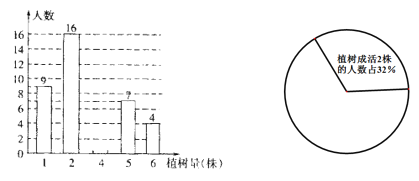
（1）请你将该条形统计图补充完整。
（2）若植树成活6株的同学中只有一名男生，学校将选择其中的两名同学为大家介绍植树经验，请用树状图或列表法表示出所有可能的结果，并求出恰好抽到一名男生和一名女生的概率.
【答案】(1)见解析；（2）
【解析】
（1）植树成活2株的人数占32％，即16人占总人数的32％，所以总人数为16÷32％=50人，则植树成活4株的人数为：50-9-16-7-4=14（人）.
(2)植树为6棵的人数一共有4人，假设这4人分别是男，女1，女2，女3，选择其中的两名同学为大家介绍植树经验，则所有可能的结果为12种，其中恰好抽到一名男生和一名女生的所有可能性为6种，则抽到一名男生和一名女生的所有可能的概率为
=
.
解：（1）16÷32％-9-16-7-4=14（人）.
（2）列表：
| 男 | 女1 | 女2 | 女3 |
男 | （男 ，女1） | （男 ， 女2） | （男， 女3） | |
女1 | （女1，男） | （女1，女2） | （女1，女3） | |
女2 | （女2，男） | （女2，女1） | （女2，女3） | |
女3 | （女3，男） | （女3，女1） | （女3，女2） |
由列表法可知：共产生12种结果，每种结果出现的可能性相同，其中出现一名男生一名女生的有6种分别为：（女1， 男），（女2，男），（女3，男）， （男，女1），（男，女2），（男，女3）.
∴P（一男一女）==.
新思维假期作业寒假吉林大学出版社系列答案
【题目】为落实视力保护工作，某校组织七年级学生开展了视力保健活动．活动前随机测查了30名学生的视力，活动后再次测查这部分学生的视力．两次相关数据记录如下：
活动前被测查学生视力数据：
（1）4.0 4.1 4.1 4.2 4.2 4.3 4.3 4.4 4.4 4.4 4.5 4.5 4.6 4.6 4.6
（2）4.7 4.7 4.7 4.7 4.8 4.8 4.8 4.8 4.8 4.9 4.9 4.9 5.0 5.0 5.1
活动后被测查学生视力数据：
（2）4.0 4.2 4.3 4.4 4.4 4.5 4.5 4.6 4.6 4.6 4.7 4.7 4.7 4.7 4.8
（3）4.8 4.8 4.8 4.8 4.8 4.8 4.9 4.9 4.9 4.9 4.9 5.0 5.0 5.1 5.1
活动后被测查学生视力频数分布表
分组 | 频数 |
| 1 |
| 2 |
| b |
| 7 |
| 12 |
| 4 |
根据以上信息回答下列问题：
（1）填空：
______，
______，活动前被测查学生视力样本数据的中位数是______，活动后被测查学生视力样本数据的众数是______；
（2）若视力在4.8及以上为达标，估计七年级600名学生活动后视力达标的人数有多少？
（3）分析活动前后相关数据，从一个方面评价学校开展视力保健活动的效果．
