题目内容
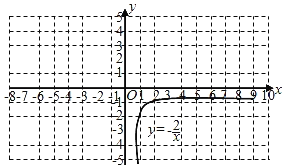
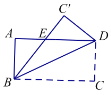
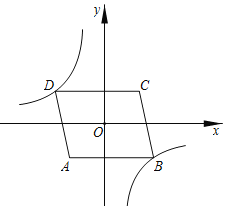
【题目】如图,在平面直角坐标系中,O为□ABCD的对称中心,点A的坐标为(-2,-2),AB=5,AB//x轴,反比例函数![]() 的图象经过点D,将□ABCD沿y轴向下平移,使点C的对应点C'落在反比例函数的图象上,则平移过程中线段AC扫过的面积为( )
的图象经过点D,将□ABCD沿y轴向下平移,使点C的对应点C'落在反比例函数的图象上,则平移过程中线段AC扫过的面积为( )
A.24B.20C.18D.14
【答案】B
【解析】
根据O为ABCD的对称中心,点A的坐标为(-2,-2),AB=5,AB∥x轴,可求点B、D、C的坐标,进而求出反比例函数的关系式,由平移可求出点C′的坐标,知道平移的距离,即平行四边形的底,再根据点的坐标,可求出平行四边形的高,最后根据面积公式求出结果.
解:∵点A的坐标为(-2,-2),AB=5,AB∥x轴,
∴B(3,-2),
∵O为ABCD的对称中心,
∴D(-3,2),C(2,2),
将D点坐标代入反比例函数的关系式得,![]()
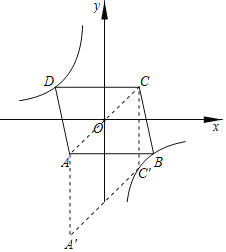
将ABCD沿y轴向下平移,使点C的对应点C′落在反比例函数的图象上,
平移后,如图, 当x=2时,![]()
∴点C′(2,-3),
∴CC′=2-(-3)=5,
![]() 上的高为:
上的高为:![]()
∴平行四边形ACC′A′的面积为5×4=20,
故选:B.

练习册系列答案
相关题目