题目内容
【题目】一次函数y=kx+b（k≠0）的图象经过点A（2，-6），且与反比例函数y=-
的图象交于点B（a，4）
（1）求一次函数的解析式；
（2）将直线AB向上平移10个单位后得到直线l：y1=k1x+b1（k1≠0），l与反比例函数y2= 
的图象相交，求使y1＜y2成立的x的取值范围．
【答案】（1）一次函数的解析式为y=-2x-2．（2）见解析
【解析】
（1）根据点B的纵坐标利用反比例函数图象上点的坐标特征可求出点B的坐标，根据点A、B的坐标利用待定系数法即可求出直线AB的解析式；
（2）根据“上加下减”找出直线l的解析式，联立直线l和反比例函数解析式成方程组，解方程组可找出交点坐标，画出函数图象，根据两函数图象的上下位置关系即可找出使y1＜y2成立的x的取值范围．
（1）∵反比例函数y=-
的图象过点B（a，4），
∴4=-
，解得：a=-3，
∴点B的坐标为（-3，4）．
将A（2，-6）、B（-3，4）代入y=kx+b中，
，解得： 
，
∴一次函数的解析式为y=-2x-2．
（2）直线AB向上平移10个单位后得到直线l的解析式为：y1=-2x+8．
联立直线l和反比例函数解析式成方程组，
，解得：
，
，
∴直线l与反比例函数图象的交点坐标为（1，6）和（3，2）．
画出函数图象，如图所示．
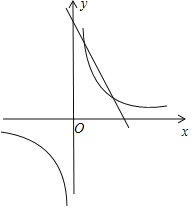
观察函数图象可知：当0＜x＜1或x＞3时，反比例函数图象在直线l的上方，
∴使y1＜y2成立的x的取值范围为0＜x＜1或x＞3．
练习册系列答案
相关题目
