题目内容
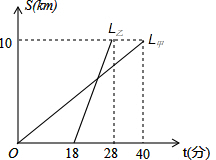 甲乙两人以相同路线前往距离单位10km的培训中心参加学习,图中L甲、L乙分别表示甲乙两人前往目的地所走的路程s(km)随时间t(分)变化的函数图象,试求多少分钟后,两人相遇?
甲乙两人以相同路线前往距离单位10km的培训中心参加学习,图中L甲、L乙分别表示甲乙两人前往目的地所走的路程s(km)随时间t(分)变化的函数图象,试求多少分钟后,两人相遇?考点:一次函数的应用
专题:
分析:设 L甲的解析式为s=kt,代入点(40,10)求出函数解析式;直线L乙的解析式为s=mt+b,代入点(18,0)、(28,10)求出函数解析式;求相遇时间两个函数联立方程求得t的数值即可.
解答:解:设L甲的解析式为s=kt,代入点(40,10)解得k=
,
∴直线L甲的解析式为s=
t,
直线L乙的解析式为s=mt+b,代入点(18,0)、(28,10)解得m=1,b=-18,
∴直线L乙的解析式为s=t-18;
t=t-18
∴t=24,
答:甲走24分钟(或乙走6分钟)时两人相遇.
| 1 |
| 4 |
∴直线L甲的解析式为s=
| 1 |
| 4 |
直线L乙的解析式为s=mt+b,代入点(18,0)、(28,10)解得m=1,b=-18,
∴直线L乙的解析式为s=t-18;
| 1 |
| 4 |
∴t=24,
答:甲走24分钟(或乙走6分钟)时两人相遇.
点评:此题主要考查了一次函数的应用,读函数的图象时首先要理解横纵坐标表示的含义结合图象上点的坐标得出是解题关键.

练习册系列答案
相关题目
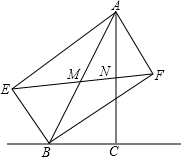 如图,BF,BE分别是∠ABC及它的邻补角∠EBG的平分线,AE⊥BE于E,AF⊥BF于F,EF分别交AB,AC于 M,N.求证:
如图,BF,BE分别是∠ABC及它的邻补角∠EBG的平分线,AE⊥BE于E,AF⊥BF于F,EF分别交AB,AC于 M,N.求证: