题目内容
如图,已知反比例函数y= 的图象经过点A(-
的图象经过点A(- ,b),过点A作AB⊥x轴,垂足为点B,△AOB的面积为
,b),过点A作AB⊥x轴,垂足为点B,△AOB的面积为 .
.(1)求k和b的值;
(2)若一次函数y=ax+1的图象经过点A,并且与x轴相交于点M,求OA:OM.

【答案】分析:(1)根据点A(-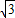 ,b)知OB=
,b)知OB=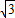 ,由△AOB的面积为
,由△AOB的面积为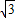 求出b,再由A点坐标求出k;
求出b,再由A点坐标求出k;
(2)由一次函数y=ax+1的图象经过点A求出a,得函数解析式,再求M的坐标,得OM的长;在△AOB中求OA的长,最后求比值.
解答:解:(1)根据题意得: ×
×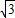 b=
b=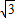 ,b=2,
,b=2,
∴A(- ,2)因为反比例函数y=
,2)因为反比例函数y= 的图象经过点A,
的图象经过点A,
∴k=-2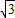 ;
;
(2)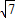 :
: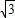 .
.
∵一次函数y=ax+1的图象经过点A,
∴- a+1=2,a=-
a+1=2,a=-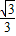 ,函数解析式为y=-
,函数解析式为y=-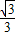 x+1,
x+1,
当y=0时,x=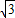 ,即OM=
,即OM= ,
,
在Rt△AOB中,OA=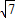 ,
,
∴OA:OM= :
: .
.
点评:此题重在检测函数解析式的求法及交点的求法.解答本题时同学们要结合图象,正确解答.
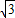 ,b)知OB=
,b)知OB=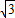 ,由△AOB的面积为
,由△AOB的面积为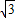 求出b,再由A点坐标求出k;
求出b,再由A点坐标求出k;(2)由一次函数y=ax+1的图象经过点A求出a,得函数解析式,再求M的坐标,得OM的长;在△AOB中求OA的长,最后求比值.
解答:解:(1)根据题意得:
 ×
×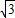 b=
b=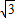 ,b=2,
,b=2,∴A(-
 ,2)因为反比例函数y=
,2)因为反比例函数y= 的图象经过点A,
的图象经过点A,∴k=-2
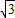 ;
;(2)
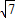 :
: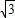 .
.∵一次函数y=ax+1的图象经过点A,
∴-
 a+1=2,a=-
a+1=2,a=-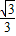 ,函数解析式为y=-
,函数解析式为y=-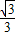 x+1,
x+1,当y=0时,x=
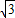 ,即OM=
,即OM= ,
,在Rt△AOB中,OA=
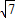 ,
,∴OA:OM=
 :
: .
.点评:此题重在检测函数解析式的求法及交点的求法.解答本题时同学们要结合图象,正确解答.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图,已知反比例函数
如图,已知反比例函数 如图,已知反比例函数
如图,已知反比例函数 如图,已知反比例函数y=
如图,已知反比例函数y= 如图,已知反比例函数
如图,已知反比例函数 如图,已知反比例函数y=
如图,已知反比例函数y=